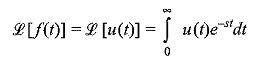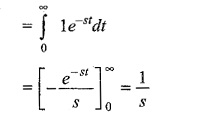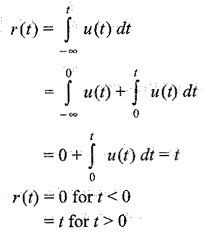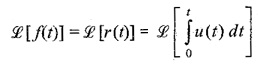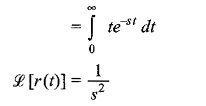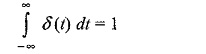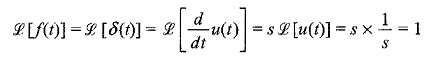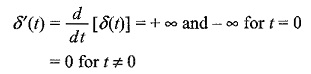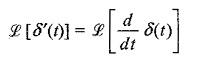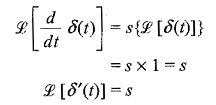Unit Step Function | Unit Ramp Function | Unit Impulse Function | Unit Doublet Function:
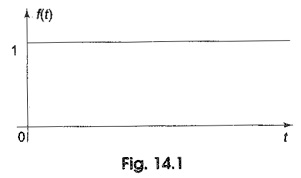
a) Unit step function: This function has already been discussed in the preceding It is defined as one that has magnitude of one for time greater than zero, and has zero magnitude for time less than zero.
A unit step function is defined mathematically as
The function is represented as shown in Fig. 14.1.
The Laplace transform of the unit step function is
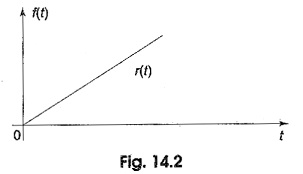
(b) Unit ramp function: If the unit step function is integrated with respect to time t, then the unit ramp function results. It is symbolized by r(t). A unit ramp function increases linearly with time. A unit ramp functions may be defined mathematically as
The function is represented as shown in Fig. 14.2.
The Laplace transform of the unit ramp function is
(c) Unit impulse function: If a unit step function u(t) is differentiated with respect to t, the derivative is zero for time t greater than zero, and is infinite for time t equal to zero. Mathematically, the function is defined as
and
where the symbol δ(t) (delta) is used to represent the unit impulse. An impulse of unity amplitude occurring at it t = 0 gives that it has an area ‘δ’ equal to unity. The unit impulse function is represented as shown in Fig. 14.3.
The Laplace transform of the unit impulse function is
Therefore
(d)Unit doublet function: If a unit impulse function δ(t) is differentiated with respect to t, we get
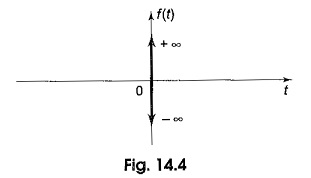
This function is called unit doublet, where δ′(t) is the symbol used to represent the unit doublet.
The unit doublet is shown in Fig. 14.4.
The Laplace transform of the unit doublet is
where δ(t) is a unit impulse occurring at t = 0.