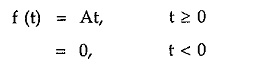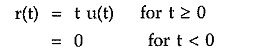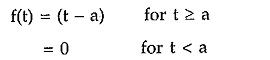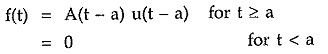Ramp Function:
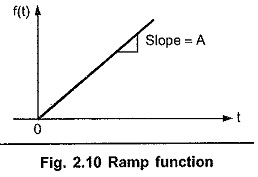
The ramp function is shown in the Fig. 2.10.
Mathematically such a function is expressed as,
Thus it is a straight line of slope A. This slope A is called amplitude or magnitude of ramp functions.
Unit Ramp Function [r(t)]:
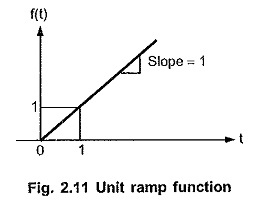
The ramp functions with unity slope i.e. having magnitude of one always, is called unit ramp function and denoted as r(t). It is shown in the Fig. 2.11.
As magnitude A of such function is always unity, mathematically it is expressed as,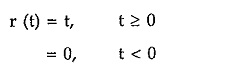
As seen earlier, any waveform if multiplied by unit step function does not change its value. Hence unit ramp functions is expressed as,
A straight line f(t) = At actually exists for all positive and negative values of t and hence mathematically occupies first and third quadrant. Practically in the network analysis t = 0 is considered as the reference time. Hence the waveforms existing for any t less than the reference time (t = 0) are not to be considered for the network analysis purpose. Hence it is necessary to suppress such waveforms, existing mathematically for all values of t less than the reference time. Hence the ramp, mathematically existing in third quadrant for t < 0 should be suppressed. Unit step function is the one which exists only for t greater than equal to reference time. And it is zero for any negative value of argument in the bracket. Hence to suppress the ramp in third quadrant it is multiplied by unit step function u (t). This is physical significance of multiplication by u(t) to the waveforms.
Similarly the ramp of magnitude A can be expressed interms of unit step function as,
where t u (t) is unit ramp functions and A is the slope of the ramp function f(t).
Shifted Unit Ramp Function:
Similar to the shifted step, the ramp functions can also shift. Such a shifted ramp is also called delayed ramp function. It is shown in the Fig. 2.12.
The shifted ramp shown is starting at t = a. Its slope is always unity as it is unit ramp functions. Such a ramp is expressed as,
Such a delayed ramp can be expressed using delayed unit step function, by the same amount.
where u(t – a) = Unit step function delayed at t = a.
The shifted ramp function having magnitude A can be expressed as,
The delayed unit ramp functions is also denoted as r(t – a).
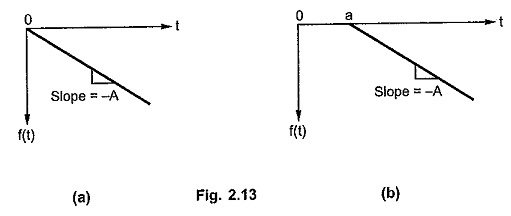
The Fig. 2.13 (a) shows the ramp with negative slope -A while the Fig. 2.13 (b) shows the delayed ramp with negative slope – A.
The ramp in Fig. 2.13 (a) is represented as,
while the ramp in Fig. 2.13 (b) is represented as,
where t u(t) is unit ramp functions and (t – a)u(t – a) is shifted unit ramp function.
Addition of two ramp functions:
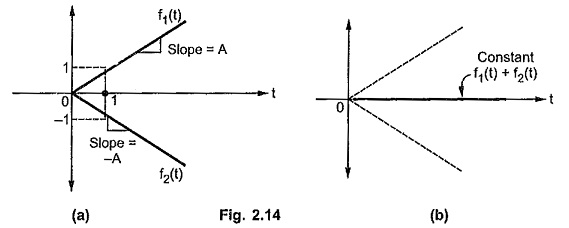
Consider the two ramp functions having equal but opposite slopes i.e. A and -A as shown in the Fig. 2.14 (a).
If such two ramps are added together, then for every t > 0 they cancel each other to produce a constant valued function as shown in the Fig. 2.14 (b).
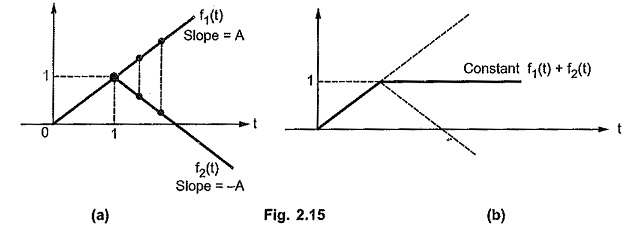
Now consider a ramp f1(t) as shown in the Fig. 2.15 (a) having slope A.
And another ramp f2(t), of same slope but with opposite sign i.e. -A is added to the initial ramp f1(t) at the instant t = 1.
After addition of such two ramps, the resulting function has a constant value equal to 1 for all t >1. This is because the two ramps cancel each other for all t > 1. This is shown in the Fig. 2.15 (b).
From the above two cases it can be concluded that the addition of two ramps having same slopes with opposite signs produces a function of constant value, for all t greater than or equal to the instant at which the two ramps are added.