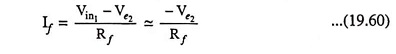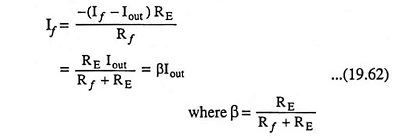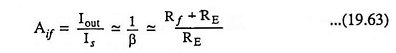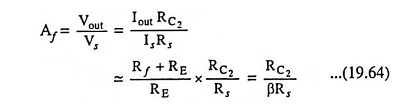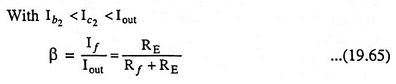Current Shunt Feedback Amplifier Circuit:

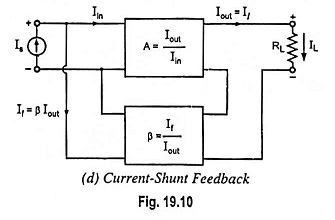
Current Shunt Feedback Amplifier Circuit is also known as series-derived shunt fed feedback or current shunt inverse feedback. In this circuit, the feedback network picks up a part of the output current and produces a feedback voltage in parallel with the input signal voltage, as shown in Fig. 19.10(d). Since the feedback shunts the input so input impedance is reduced with feedback whereas output impedance is increased because of feedback network being in series with the output.

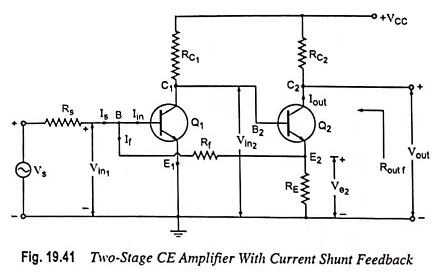
A two-stage cascaded amplifier using such a feedback is given in Fig. 19.41. Here feedback is from the emitter of second stage to the base of first stage through resistor R_f. In this input voltage (V_in2) to second stage is much larger than input voltage (V_in1) to first stage, because of amplifying action of transistor Q₁, and is in phase opposition to it (i.e., phase difference of 180°). Voltage V_e2 is only slightly smaller than V_in2, because of emitter follower action. Also voltages V_e2 and V_in2 are in phase. Thus V_e2 is larger in magnitude than V_in1 and has a phase difference of 180° with V_in1. When input signal increases causing I_s to increase, feedback current I_f also increases and so the input current V_in1 would be smaller than it would be without feedback as it is difference of I_s and I_f. Thus negative feedback is provided.

With R_f much larger than R_E, the circuit shown in Fig. 19.41 approximates a current-shunt feedback pair and feedback current I_f is given as

because V_in1 is quite small as compared to V_e2

Neglecting base current of transistor Q₂ in comparison to its collector current and assuming R_f >> R_E

and so

Since feedback current is proportional to the output current, this circuit is an example of a Current Shunt Feedback Amplifier.

Transfer current gain with feedback,

Thus transfer current gain A_if would be stable provided that resistors R_E and R_f are stable.

Assuming input impedance with feedback R_inf to be zero, V_s = I_sR_s

and the voltage gain with feedback,

Thus voltage gain with feedback is stable i.e., independent of the transistor parameters, the temperature, or supply voltage variations because resistors R_f, R_E, R_C2 and R_S are stable elements.

Amplifier Without Feedback:

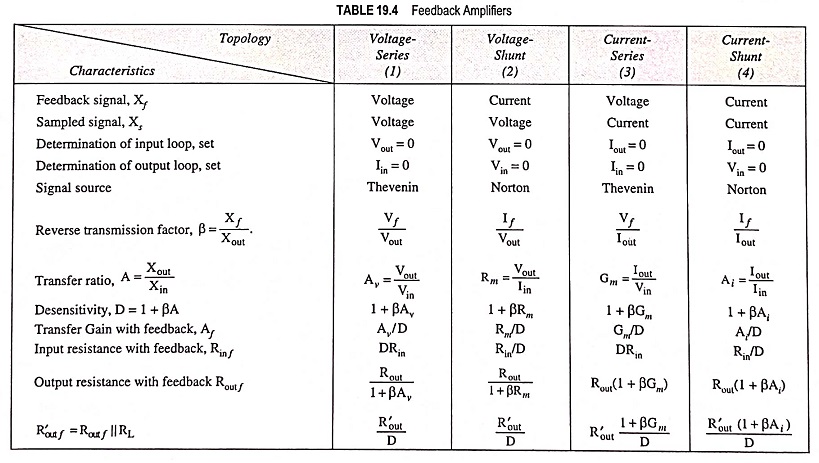
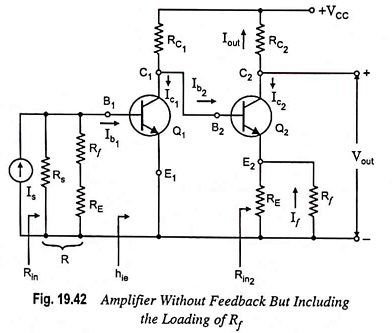
Referring to the fourth topology in Table 19.4, the input circuit of the amplifier without feedback is obtained by opening the output loop at the emitter of Q₂. This places R_f in series with R_E from base to emitter of Q₁. The output circuit is obtained by shorting the input node (base of Q₁). This places R_f in parallel with R_E. The resultant equivalent circuit is shown in Fig. 19.42. Since the feedback signal is a current, the source is represented by a Norton’s equivalent circuit with

The feedback signal is the current I_f in the resistor R_f, which is in the output circuit.

From Fig. 19.42,

which is in agreement with Eq. (19.62).