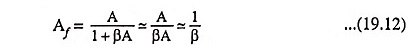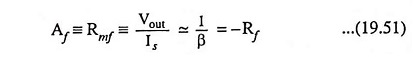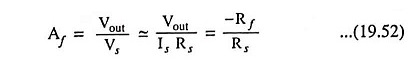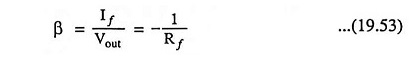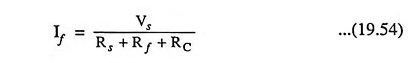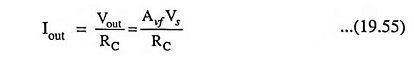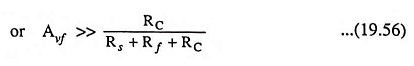Voltage Shunt Feedback Amplifier Circuit:
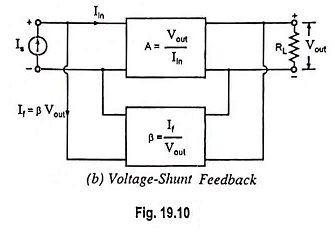
Voltage Shunt Feedback Amplifier Circuit is also known as shunt-derived shunt fed feedback or voltage shunt inverse feedback. Here, a small portion of the output voltage is coupled back to the input voltage, as shown in Fig. 19.10 (b). Since the feedback network shunt both the input and output of the amplifier, both of the input and output impedances are reduced by a factor 1/(1 + βA).
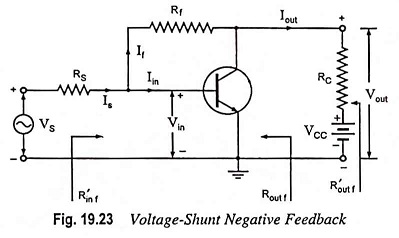
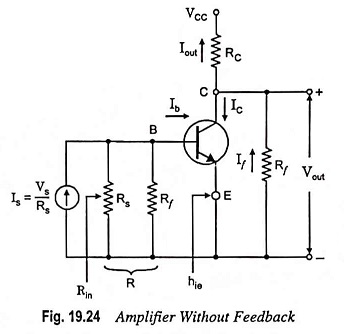
Figure 19.23 gives the circuit of a common-emitter amplifier stage with a resistor Rf providing feedback from collector to base. Here the feedback is proportional to the output voltage Vout and feedback current If gets added in shunt with the input. Thus this circuit forms the case of voltage-shunt inverse feedback amplifier.
From circuit shown in Fig. 19.23.
Feedback current,
From Eqs. (19.12) and (19.50) and assuming Is ≈ If
Thus the transresistance equals the negative of the feedback resistance from output to input of the transistor and is stable if Rf is a stable resistance. Both the input and output resistances are reduced because the feedback network shunts both the input and output of the amplifier. Assuming input impedance to be zero, voltage gain with feedback.
Thus if resistors Rf and Rs are stable elements, then voltage gain is stable (independent of the transistor parameters, the temperature or supply voltage variations).
Amplifier Without Feedback:
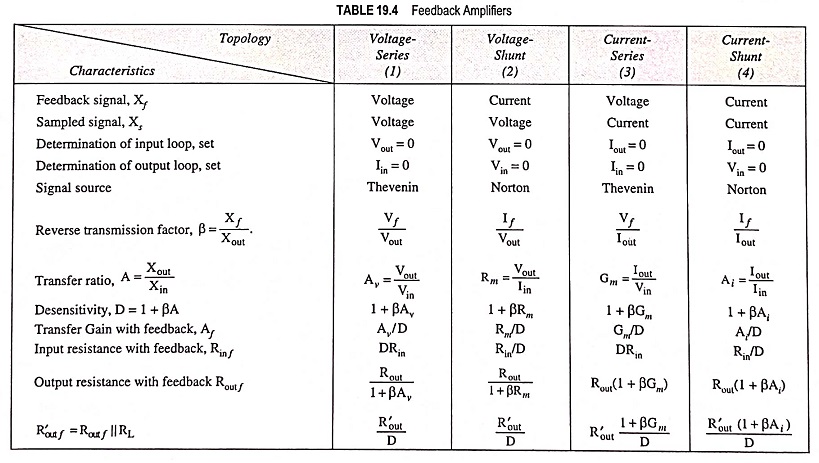
Referring to second topology in Table 19.4, the input circuit of the amplifier without feedback is obtained by setting Vout = 0 (shorting the output node). Thus connecting resistor Rf from base to emitter of the transistor. The output circuit is obtained by setting Vin = 0 (shorting the input node), thus connecting Rf from collector to emitter. Thus, the amplifier circuit without feedback is depicted in Fig. 19.24. Since the feedback signal is a current, the source is represented by a Norton’s equivalent with Is = Vs/Rs.
The feedback signal is the current If in the feedback resistor Rf which is the output circuit.
From Fig. 19.24,
If the amplifier is deactivated by reducing hfe to zero, a current If passes through the β network (the resistor Rf) from input to output and this current is
The output current Iout with the amplifier activated is
So the condition that the forward transmission through the feedback network can be neglected is Iout >> If
Since this voltage gain is at least unity, this inequality is easily satisfied by selecting (Rs + Rf) >> RC.