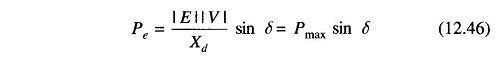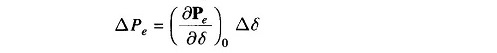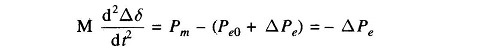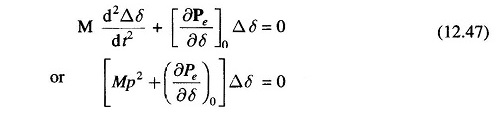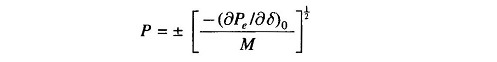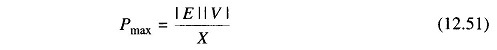Steady State Stability in Power System:
The steady state stability limit of a particular circuit of a power system is defined as the maximum power that can be transmitted to the receiving end without loss of synchronism.
Consider the simple system of Fig. 12.14 whose dynamics is described by equations
and
For determination of Steady State Stability in Power System, the direct axis reactance (Xd) and voltage behind Xd are used in the above equations.
The plot of Eq. (12.46) is given in Fig. 12.6. Let the system be operating with steady power transfer of Pe0 = Pm with torque angle δ0 as indicated in the figure. Assume a small increment ΔP in the electric power with the input from the prime mover remaining fixed at Pm (governor response is slow compared to the speed of energy dynamics), causing the torque angle to change to (δ0 + Δδ) Linearizing about the operating point Q0 (Pe0, δ0) we can write
The excursions of Δδ are then described by
or
Where
The system stability to small changes is determined from the characteristic equation
whose two roots are
As long as (∂Pe/∂δ)0 is positive, the roots are purely imaginary and conjugate and the system behavior is oscillatory about δ0. Line resistance and damper windings of machine, which have been ignored in the above modelling, cause the system oscillations to decay. The system is therefore stable for a small increment in power so long as
When (∂Pe/∂δ)0 is negative, the roots are real, one positive and the other negative but of equal magnitude. The torque angle therefore increases without bound upon occurrence of a small power increment (disturbance) and the synchronism is soon lost. The system is therefore unstable for
(∂Pe/∂δ)0 is known as synchronizing coefficient. This is also called stiffness (electrical) of synchronous machine.
Assuming |E| and |V| to remain constant, the system is unstable, if
The maximum power that can be transmitted without loss of stability (steady state) occurs for
and is given by
If the system is operating below the limit of steady stability condition (Eq. 12.48), it may continue to oscillate for a long time if the damping is low. Persistent oscillations are a threat to system security. The study of system damping is the study of dynamical stability.
The above procedure is also applicable for complex systems wherein governor action and excitation control are also accounted for. The describing differential equation is linearized about the operating point. Condition for Steady State Stability in Power System is then determined from the corresponding characteristic equation (which now is of order higher than two).
It was assumed in the above account that the internal machine voltage |E| remains constant (i.e., excitation is held constant). The result is that as loading increases, the terminal voltage |Vt| dips heavily which cannot be tolerated in practice. Therefore, we must consider the steady state stability limit by assuming that excitation is adjusted for every load increase to keep |Vt| constant. This is how the system will be operated practically. It may be understood that we are still not considering the effect of automatic excitation control.