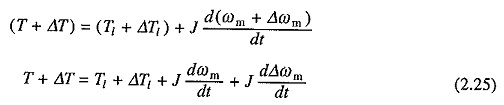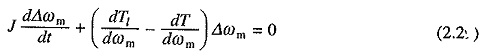Steady State Stability of Drive:
Equilibrium speed of a motor-load system is obtained when motor torque equals the load torque. Drive will operate in steady-state at this speed, provided it is the speed of stable equilibrium. Concept of Steady State Stability of Drive has been developed to readily evaluate the stability of an equilibrium point from the steady-state speed-torque curves of the motor and load, thus avoiding solution of differential equations valid for transient operation of the drive.
In most drives, the electrical time constant of the motor is negligible compared to its mechanical time constant. Therefore, during transient operation, motor can be assumed to be in electrical equilibrium implying that steady-state speed-torque curves are also applicable to the transient operation.
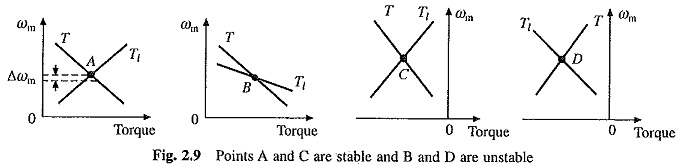
As an example let us examine the Steady State Stability of Drive of equilibrium point A in Fig. 2.9(a). The equilibrium point will be termed as stable when the operation will be restored to it after a small departure from it due to a disturbance in the motor or load. Let the disturbance causes a reduction of Δωm in speed. At new speed, motor torque is greater than the load torque, consequently, motor will accelerate and operation will be restored to A. Similarly, an increase of Δωm in speed caused by a disturbance will make load torque greater than the motor torque, resulting into deceleration and restoration of operation to point A. Hence the drive is steady-state stable at point A.
Let us now examine equilibrium point B which is obtained when the same motor drives another load. A decrease in speed causes the load torque to become greater than the motor torque, drive decelerates and operating point moves away from B. Similarly, when working at B an increase in speed will make motor torque greater than the load torque, which will move the operating point away from B. Thus, B is an unstable point of equilibrium. Readers may similarly examine the Steady State Stability of Drive of points C and D given in Figs. 2.9(c) and (d).
Above discussion suggests that an equilibrium point will be stable when an increase in speed causes load-torque to exceed the motor torque, i.e. when at equilibrium point following condition is satisfied:
Inequality (2.24) can be derived by an alternative approach. Let a small perturbation in speed, Δωm, results in ΔT and ΔTl perturbations in T and Tl respectively. Then from Eq. (2.2)
Subtracting (2.2) from (2.25) and rearranging terms gives
For small perturbations, the speed torque curves of the motor and load can be assumed to be straight lines. Thus
where (dT/dωm) and (dTl/dωm) are respectively slopes of the steady-state speed-torque curves of motor and load at operating point under consideration. Substituting Eqs. (2.27) and (2.28) into (2.26) and rearranging the terms yields
This is a first order linear differential equation. If initial deviation in speed at t = 0 be (Δωm)0 then the solution of Eq. (2.29) will be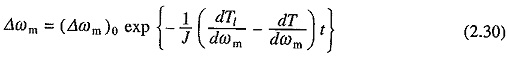
An operating point will be stable when Δωm approaches zero as t approaches infinity. For this to happen the exponent in Eq. (2.30) must be negative. This yields the inequality of Eq. (2.24).