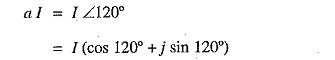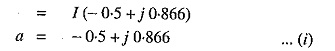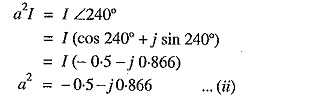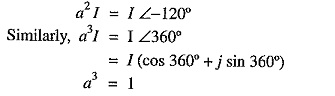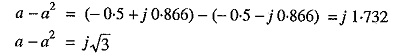Unsymmetrical Faults on Three Power System:

Those faults on the power system which give rise to unsymmetrical fault currents (i.e. unequal fault currents in the lines with unequal phase displacement) are known as Unsymmetrical Faults on Three Power System.

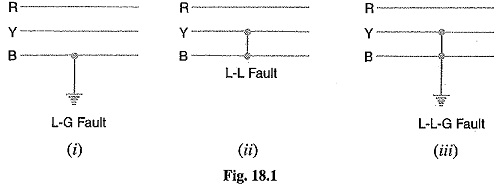
On the occurrence of an Unsymmetrical Faults on Three Power System, the currents in the three lines become unequal and so is the phase displacement among them. It may be noted that the term `unsymmetry’ applies only to the fault itself and the resulting line currents. However, the system impedances and the source volt­ages are always symmetrical through its main elements viz. generators, transmission lines, synchoronous reactors etc. There are three ways in which unsymmetrical faults may occur in a power system (see Fig. 18.1).

1. Single line-to-ground fault (L — G)
2. Line-to-line fault (L — L)
3. Double line-to-ground fault (L — L— G)

The Solutions of Unsymmetrical Faults on Three Power System problems can be obtained by either (a) Kirchhoff’s laws or (b) Symmetrical components method. The latter method is preferred because of the following reasons :

• It is a simple method and gives more generality to be given to fault performance studies.
• It provides a useful tool for the protection engineers, particularly in connection with tracing out of fault currents.

Symmetrical Components Method:

In 1918, Dr. C.L. Fortescue, an American scientist, showed that any unbalanced system of 3-phase currents (or voltages) may be regarded as being composed of three separate sets of balanced vectors viz.

• balanced system of 3-phase currents having positive (or normal) phase sequence. These are called positive phase sequence components.
• a balanced system of 3-phase currents having the opposite or negative phase sequence. These are called negative phase sequence components.
• a system of three currents equal in magnitude and having zero phase displacement. These are called zero phase sequence components.

The positive, negative and zero phase sequence components are called the symmetrical compo­nents of the original unbalanced system. The term ‘symmetrical’ is appropriate because the unbal­anced 3-phase system has been resolved into three sets of balanced (or symmetrical) components. The subscripts 1, 2 and 0 are generally used to indicate positive, negative and zero phase sequence components respectively. For instance, I_R0 indicates the zero phase sequence component of the current in the red phase. Similarly, I_Y1 implies the positive phase sequence component of current in the yellow phase.

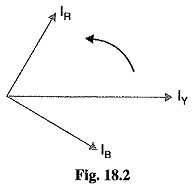
Let us now apply the symmetrical components theory to an unbalanced 3-phase system. Suppose an Unsymmetrical Faults on Three Power System occurs on a 3-phase system having phase sequence RYB. According to symmetrical components theory, the resulting unbalanced currentes I_R,I_Y and I_B (see Fig. 18.2) can be resolved into :

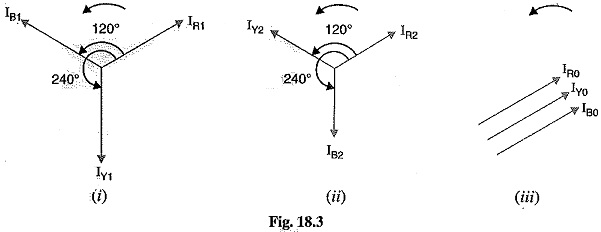
1. a balanced system of 3-phase currents, I_R1,I_Y1,I_B1 having positive phase sequence (i.e. RYB) as shown in Fig. 18.3 (i). These are the positive phase sequence components.
2. a balanced system of 3-phase currents I_R2,I_Y2,I_B2 having negative phase sequence (I e. RBY) as shown in_: 18.3 (ii). These are the negative phase sequence components.
3. a system of three currents I_R0,I_Y0,I_B0 equal in magnitude with zero phase displacement from each other as shown in Fig. 18.3 (iii). These are the zero phase sequence components.

The current in any phase is equal to the vector sum of positive, negative and zero phase sequence currents in that phase as shown in Fig. 18.4.

The following points may be noted :

• The positive phase sequence currents (I_R1,I_Y1,I_B1), negative phase sequence currents (I_R2,I_Y2,I_B2) and zero phase sequence currents (I_R0,I_Y0,I_B0) separately form balanced system of currents. Hence, they are called symmetrical components of the unbalanced system.
• The symmetrical component theory applies equally to 3-phase currents and voltages both phase and line values.
• The symmetrical components do not have separate existence. They are only mathematical components of unbalanced currents (or voltages) which actually flow in the system.
• In a balanced 3-phase system, negative and zero phase sequence currents are zero.

Operator ‘a’

As the symmetrical component theory involves the concept of 120° displacement in the positive sequence set and negative sequence set, therefore, it is desirable to evolve some operator which should cause 120° rotation. For this purpose, operator ‘a’ (symbols h or λ are sometimes used instead of ‘a’) is used. It is defined as under :

The operator ‘a’ is one, which when multiplied to a vector rotates the vector through 120° in the anticlockwise direction.

Consider a vector I represented by OA as shown in Fig. 18.5. If this vector is multiplied by operator ‘a’, the vector is rotated through 120° in the anticlockwise direction and assumes the posi­tion OB.

If the vector assuming position OB is multiplied by operator ‘a’, the vector is further rotated through 120° in the anticlockwise direction and assumes the position OC.

Thus the operator ‘a^2, will turn the vector through 240° in the anticlockwise direction. This is the same as turning the vector through 120° in clockwise direction.

Properties or Operator ‘a’

1. Adding exps. (i) and (ii), we get,

2. Subtracting exp. (ii) from exp. (i), we get,