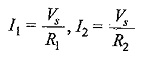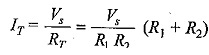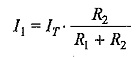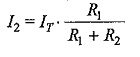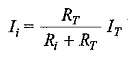Current Divider Equation:

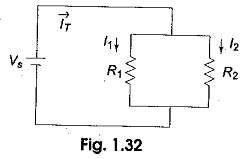
In a parallel circuit, the Current Division in all branches. Thus, a parallel circuit acts as a current divider. The total current entering into the parallel branches is divided into the branches currents according to the resistance values. The branch having higher resistance allows lesser current, and the branch with lower resistance allows more current. Let us find the Current Divider Equation in the parallel circuit shown in Fig. 1.32.

Current Divider Equation

The voltage applied across each resistor is Vs. The current passing through each resistor is given by

Current Divider Equation

If RT is the total resistance, which is given by R1R2/(R1+R2),

Total currentCurrent Divider Equation

Current Divider Equation

Similarly,

From the above equations, we can conclude that the current in any branch is equal to the ratio of the opposite branch resistance to the total resistance value, multiplied by the total current in the circuit. In general, if the circuit consists of m branches, the Current Divider Equation in any branch can be determined by

Current Divider Equation

where

  • Ii represents the current in the ith branch
  • Ri is the resistance in the ith branch
  • RT is the total parallel resistance to the ith branch and
  • IT is the total current entering the circuit.

Formula of Power in Parallel Circuit:

The total power supplied by the source in any parallel resistive circuit is equal to the sum of the powers in each resistor in parallel, i.e.

Formula of Power in Parallel Circuit

where m is the number of resistors in parallel,Ps is the total power and Pm is the power in the last resistor.

Related posts:

  1. Voltage and Current Divider Rule
  2. FET Biasing Methods – Fixed Bias, Self Bias, Potential Divider Bias and Current Source Bias
  3. Townsend Current Growth Equation
  4. Mesh Current Equation
  5. Voltage Divider Circuit Diagram
  6. Mixed RC Potential Divider
  7. Low Voltage Arms for Voltage Divider
  8. Voltage Divider Bias Circuit
  9. Voltage Divider Bias Circuit
  10. Self Bias or Potential Divider Bias Circuit
  11. Drift Current and Diffusion Current in Semiconductor
  12. Current Controlled Current Source (CCCS) Circuit
  13. Current Collection System in Electric Traction and Types of Current Collection
  14. Torque Equation of Synchronous Motor
  15. Power Flow Equation of Synchronous Generator
  16. Torque Equation of DC Motor
  17. General Equation for Electromagnetic Relay
  18. Non Homogeneous Differential Equation
  19. Tuned Collector Oscillator – Definition, Working and Equation
  20. Tuned Drain Oscillator – Circuit Diagram and Equation