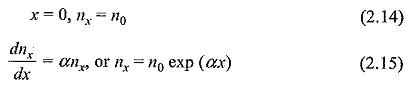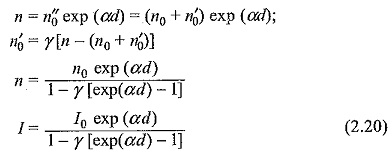Townsend Current Growth Equation:
Referring to Fig. 2.1 shows the Townsend Current Growth Equation. let us assume that n0 electrons are emitted from the cathode. When one electron collides with a neutral particle, a positive ion and an electron are formed. This is called an ionizing collision. Let α be the average number of ionizing collisions made by an electron per centimetre travel in the direction of the field (α depends on gas pressure p and E/p, and is called the Townsend’s first ionization coefficient). At any distance x from the cathode, let the number of electrons be nx. When these nx electrons travel a further distance of dx they give rise to (αnxdx) electrons.
Then, the number of electrons reaching the anode (x = d) will be
The number of new electrons created, on the average, by each electron is
Therefore, the average current in the gap, which is equal to the number of electrons travelling per second will be
where I0 is the initial current at the cathode.
Current Growth in Presence of Secondary Processes:
The single avalanche process described in the previous section becomes complete when the initial set of electrons reaches the anode. However, since the amplification of electrons [exp (αd)] is occurring in the field, the probability of additional new electrons being liberated in the gap by other mechanisms increases, and these new electrons create further avalanches. The other mechanisms are
- The positive ions liberated may have sufficient energy to cause liberation of electrons from the cathode when they impinge on it.
- The excited atoms or molecules in avalanches may emit photons, and this will lead to the emission of electrons due to photo-emission.
- The metastable particles may diffuse back causing electron emission.
The electrons produced by these processes are called secondary electrons. The secondary ionization coefficient γ is defined in the same way as α, as the net number of secondary electrons produced per incident positive ion, photon, excited particle, or metastable particle, and the total value of γ is the sum of the individual coefficients due to the three different processes, i.e. γ=γ1+γ2+γ3. γ is called the Townsend’s secondary ionization coefficient and is a function of the gas pressure p and E/p.
Following Townsend’s procedure for current growth; let us assume
n′0 = number of secondary electrons produced due to secondary ()) processes.
Let n″0 = total number of electrons leaving the cathode.
The total number of electrons n reaching the anode becomes,
Townsend’s Criterion for Breakdown:
Equation (2.20) gives the total average current in a gap before the occurrence of breakdown. As the distance between the electrodes d is increased, the denominator of the equation tends to zero, and at some critical distance d=ds.
For values of d < ds, I is approximately equal to I0 and if the external source for the supply of I0 is removed, I becomes zero. If d = ds, I→∞ and the current will be limited only by the resistance of the power supply and the external circuit. This condition is called Townsend’s breakdown criterion and can be written as
Normally, exp (αd) is very large, and hence the above equation reduces to yexp (ad) =
For a given gap spacing and at a given pressure the value of the voltage V which gives the values of α and γ satisfying the breakdown criterion is called the spark breakdown voltage Vs and the corresponding distance ds is called the sparking distance.
The Townsend Current Growth Equation explains the phenomena of breakdown only at low pressure, corresponding to p x d (gas pressure x gap distance) values of 1000 torr-cm and below.