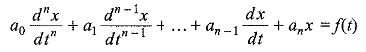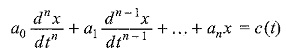Non Homogeneous Differential Equation:

Now let us consider the following Non Homogeneous Differential Equation,

where the coefficients a₀, a₁, … a_n are constants, and f(t) is a function of me.
The general solution may be written

where x_c is the complementary function, and x_p is the particular integral. Since x_c is the general solution of the corresponding homogeneous equation with f(t) replaced by zero, we have to find out the particular integral x_p.

The particular integral can be calculated by the method of undetermined coefficients. This method is useful to equations

when c(t) is such that the form of a particular solution x_p of the above equation may be guessed.

For example, c(t) may be a single power of t, a polynomial, an exponential, a sinusoidal function, or a sum of such functions. The method consists in assuming for, x_p an expression similar to that of c(t), containing unknown coefficients which are to be determined by inserting x_p and its derivatives in the original equation.