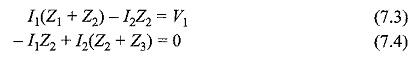Mesh Current Equation:
We have earlier discussed meth analysis but have applied it only to resistive circuits. Some of the ac circuits presented in this chapter can also be solved by using Mesh Current Equation analysis. We already know, the two basic techniques for writing network equations for mesh analysis and node analysis were presented. These concepts can also be used for sinusoidal steady-state condition.
In the sinusoidal steady-state analysis, we use voltage phasors, current phasors, impedances and admittances to write branch equations, KVL and KCL equations. For ac circuits, the method of writing loop equations is modified slightly. The voltages and currents in ac circuits change polarity at regular intervals. At a given time, the instantaneous voltages are driving in either the positive or negative direction. If the impedances are complex, the stun of their voltages is found by vector addition. We shall illustrate the method of writing network Mesh Current Equation with the following example.
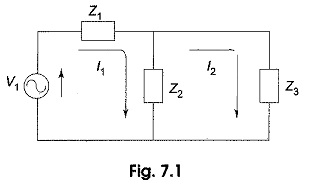
Consider the circuit shown in Fig. 7.1, containing a voltage source and impedances.
The current in impedance Z1 is I1, and the current in Z2, (assuming a positive direction downwards through the impedance) is I1 – I2. Similarly, the current in impedance Z3 is I2. By applying Kirchhoff’s voltage law for each loop, we can get two equations. The voltage across any-element is the product of the phasor current in the element and the complex impedance.
Equation for loop 1 is
Equation for loop 2, which contains no source is
By rearranging the above equations, the corresponding mesh current equations are
By solving the above equations, we can find out currents I1 and I2. In general, if we have M meshes, B branches and N nodes including the reference node, we assume M branch currents and write M independent equations; then the number of mesh currents is given by M = B – (N- 1).