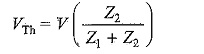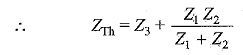Thevenin Equivalent Circuit:
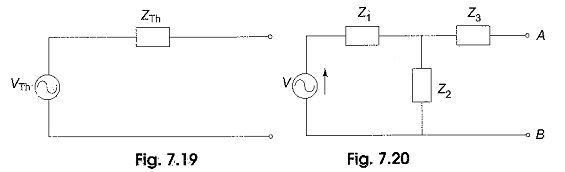
Thevenin’s theorem gives us a method for simplifying a given circuit. The Thevenin Equivalent Circuit form of any complex impedance circuit consists of an equivalent voltage source VTh, and an equivalent impedance ZTh, arranged as shown in Fig. 7.19. The values of equivalent voltage and impedance depend on the values in the original circuit.
Though the Thevenin equivalent circuit is not the same as its original circuit, the output voltage and output current are the same in both cases. Here, the Thevenin voltage is equal to the open circuit voltage across the output terminals, and impedance is equal to the impedance seen into the network across the output terminals.
Consider the circuit shown in Fig. 7.20.
Thevenin equivalent for the circuit shown in Fig. 7.20 between points A and B is found as follows.
The voltage across points A and B is the Thevenin equivalent voltage. In the circuit shown in Fig. 7.20, the voltage across A and B is the same as the voltage across Z2 because there is no current through Z3.
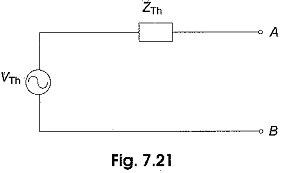
The impedance between points A and B with the source replaced by short circuit is the Thevenin equivalent impedance. In Fig. 7.20, the impedance from A to B is Z3 in series with the parallel combination of Z1 and Z2.
The Thevenin equivalent circuit is shown in Fig. 7.21.