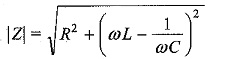Impedance and Phase Angle of Series Resonant Circuit:

The impedance of a Series Resonant Circuit is

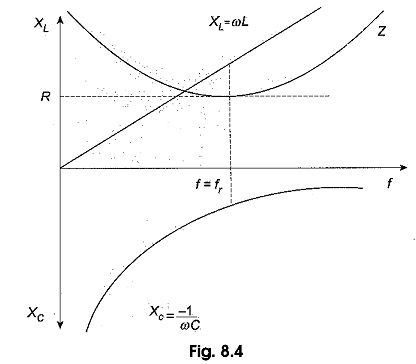
The variation of X_C and X_L with frequency is shown in Fig. 8.4.

At zero frequency, both X_C and Z are infinitely large, and X_L is zero because at zero frequency the capacitor acts as an open circuit and the inductor acts as a short circuit. As the frequency increases, X_C decreases and X_L increases. Since X_C is larger than X_L, at frequencies below the resonant frequency f_r, Z decreases along with X_C.

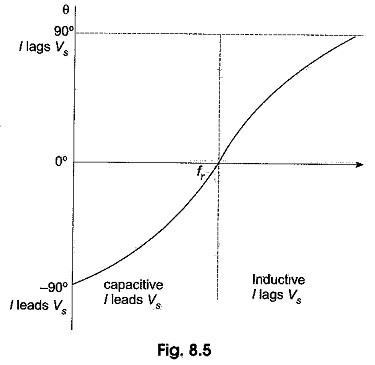
At resonant frequency f_r, X_C = X_L, and Z = R. At frequencies above the resonant frequency f_r, X_L is larger than X_C, causing Z to increase. The phase angle as a function of frequency is shown in Fig. 8.5.

At a frequency below the resonant frequency, current leads the source voltage because the capacitive reactance is greater than the inductive reactance. The phase angle decreases as the frequency approaches the resonant value, and is 0° at resonance.

At frequencies above resonance, the current lags behind the source voltage, because the inductive reactance is greater than capacitive reactance. As the frequency goes higher, the phase angle approaches 90°.