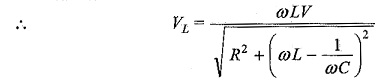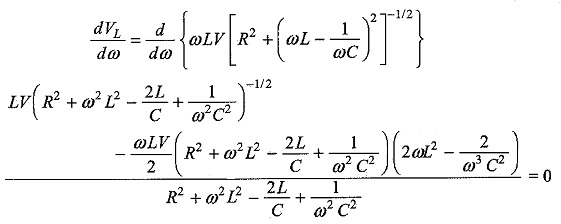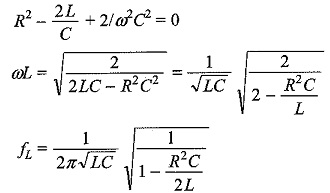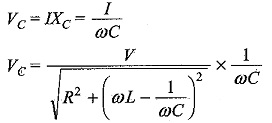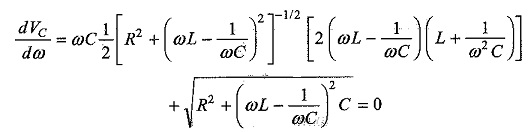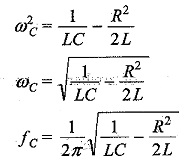Voltage and Current in Series Resonant Circuit:
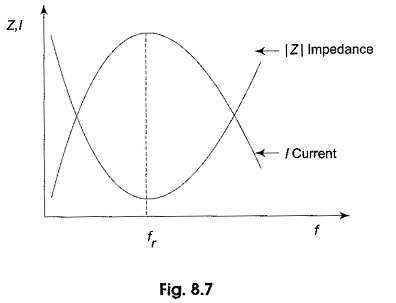
The variation of impedance and current with frequency of Voltage and Current in Series Resonant Circuit is shown in Fig. 8.7.
At resonant frequency, the capacitive reactance is equal to inductive reactance, and hence the impedance is minimum. Because of minimum impedance, maximum current flows through the circuit. The current variation with frequency is plotted.
The voltage drop across resistance, inductance and capacitance also varies with frequency. At f = 0, the capacitor acts as an open circuit and blocks current. The complete source voltage appears across the capacitor. As the frequency increases, XC decreases and XL increases, causing total reactance XC — XL to decrease. As a result, the impedance decreases and the current increases. As the current increases, VR also increases, and both VC and VL increase.
When the frequency reaches its resonant value fr, the impedance is equal to R, and hence, the current reaches its maximum value, and VR is at its maximum value.
As the frequency is increased above resonance, XL continues to increase and XC continues to decrease, causing the total reactance, XL—XC to increase. As a result there is an increase in impedance and a decrease in current. As the current decreases, VR also decreases, and both VC and VL decrease. As the frequency becomes very high, the current approaches zero, both VR and VC approach zero, and VL approaches VS.
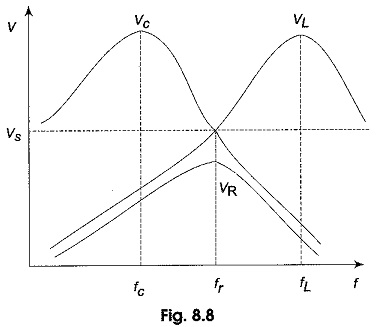
The response of different voltages with frequency is shown in Fig. 8.8.
The drop across the resistance reaches its maximum when f = fr. The maximum voltage across the capacitor occurs at f = fc. Similarly, the maximum voltage across the inductor occurs at f = fL.
The voltage drop across the inductor is
where
To obtain the condition for maximum voltage across the inductor, we have to take the derivative of the above equation with respect to frequency, and make it equal to zero.
If we solve for ω, we obtain the value of ω when VL is maximum.
From this
Similarly, the voltage across the capacitor is
To get maximum value dVc/dω = 0
If we solve for ω, we obtain the value of ω when VC is maximum.
From this
The maximum voltage across the capacitor occurs below the resonant frequency; and the maximum voltage across the inductor occurs above the resonant frequency.