Sequence Impedance and Networks of Transformers:
It is well known that almost all present day installations have three-phase transformers since they entail lower initial cost, have smaller space requirements and higher efficiency. The positive sequence series impedance of a transformer equals its leakage impedance. Since a transformer is a static device, the leakage impedance does not change with alteration of phase sequence of balanced applied voltages. The negative Sequence Impedance and Networks of Transformers is also therefore equal to its leakage reactance. Thus, for a transformer
Assuming such transformer connections that zero sequence currents can flow on both sides, a transformer offers a zero sequence impedance which may differ slightly from the corresponding positive and negative sequence values. It is, however, normal practice to assume that the series impedances of all sequences are equal regardless of the type of transformer.
The zero sequence magnetizing current is somewhat higher in a core type than in a shell type transformer. This difference does not matter as the magnetizing current of a transformer is always neglected in short circuit analysis.
Above a certain rating (1,000 kVA) the reactance and impedance of a transformer are almost equal and are therefore not distinguished.
Zero Sequence Networks of Transformers:
Before considering the zero sequence networks of various types of transformer connections, three important observations are made:
- When magnetizing current is neglected, transformer primary would carry current only if there is current flow on the secondary side.
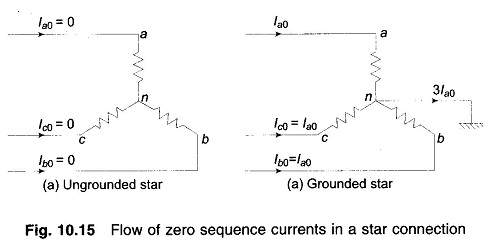
- Zero sequence currents can flow in the legs of a star connection only if the star point is grounded which provides the necessary return path for zero sequence currents. This fact is illustrated by Figs. 10.15a and b.
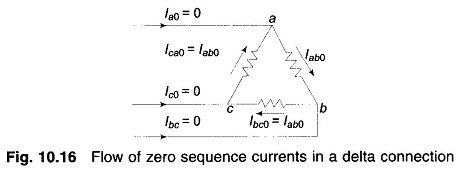
- No zero sequence currents can flow in the lines connected to a delta connection as no return path is available for these currents. Zero sequence currents can, however, flow in the legs of a delta—such currents are caused by the presence of zero sequence voltages in the delta connection. This fact is illustrated by Fig. 10.16.
Let us now consider various types of transformer connections.
Case 1: Y-Y transformer bank with any one neutral grounded:
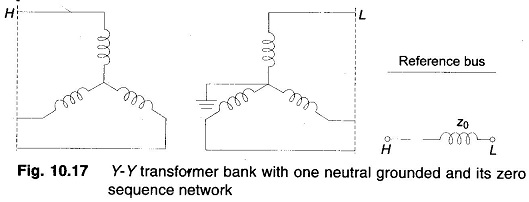
If any one of the two neutrals of a Y- Y transformer is ungrounded, zero sequence currents cannot flow in the ungrounded star and consequently, these cannot flow in the grounded star. Hence, an open circuit exists in the zero sequence network between H and L, i.e. between the two parts of the system connected by the transformer as shown in Fig. 10.17.
Case 2: Y-Y transformer bank both neutrals grounded:
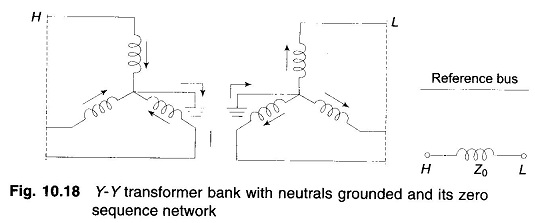
When both the neutrals of a Y—Y transformer are grounded, a path through the transformer exists for zero sequence currents in both windings via the two grounded neutrals. Hence, in the zero sequence network H and L are connected by the zero Sequence Impedance and Networks of Transformers as shown in Fig. 10.18.
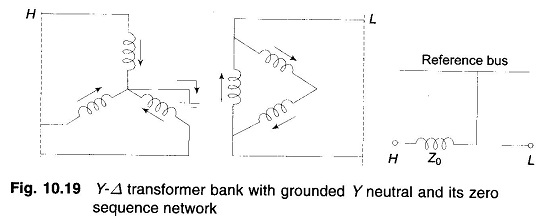
Case 3: Y-Δ transformer bank with grounded Y neutral:
If the neutral of star side is grounded, zero sequence currents can flqw in star because a path is available to ground and the balancing zero sequence currents can flow in delta. Of course no zero sequence currents can flow in the line on the delta side. The zero sequence network must therefore have a path from the line H on the star side through the zero sequence impedance of the transformer to the reference bus, while an open circuit must exist on the line L side of delta (see Fig. 10.19). If the star neutral is grounded through Zn, an impedance 3Zn appears in series with Z0 in the sequence network.
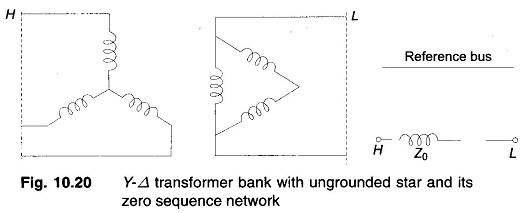
Case 4: Y-Δ transformer bank with ungrounded star:
This is the special case of Case 3 where the neutral is grounded through Zn = ∞. Therefore no zero sequence current can flow in the transformer windings. The zero sequence network then modifies to that shown in Fig. 10.20.
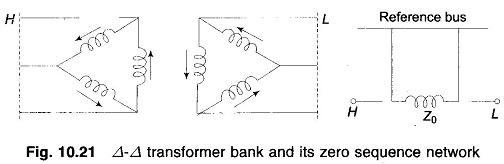
Case 5: Δ-Δ transformer bank:
Since a delta circuit provides no return path, the zero sequence currents cannot flow in or out of Δ – Δ transformer; however it can circulate in the delta windings. Therefore there is an open circuit between H and L and Z0 is connected to the reference bus on both ends to account for any circulating zero sequence current in the two deltas (see Fig. 10.21)