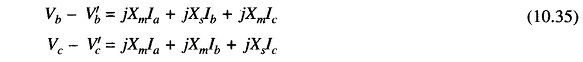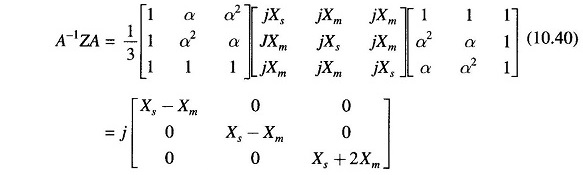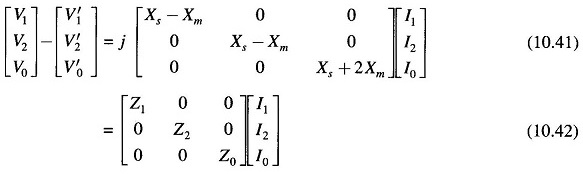Sequence Impedances of Transmission Lines:

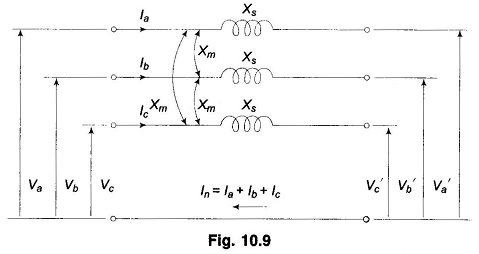
Sequence Impedances of Transmission Lines – Figure 10.9 shows the circuit of a fully transposed line carrying unbalanced currents. The return path for I_n is sufficiently away for the mutual effect to be ignored.

Let

• X_s = self reactance of each line
• X_m = mutual reactance of any line pair

The following KVL equations can be written down from Fig. 10.9.

or in matrix form

or

or

or

Now

Thus Eq. (10.37) can be written as

wherein

We conclude that a fully transposed transmission has:

• equal positive and negative Sequence Impedances of Transmission Lines.
• zero sequence impedance much larger than the positive (or negative) Sequence Impedances (it is approximately 2.5 times).

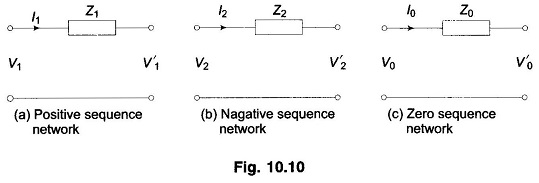
It is further observed that the sequence circuit equations (10.42) are in decoupled form, i.e. there are no mutual sequence inductances. Equation (10.42) can be represented in network form as in Fig. 10.10.

The decoupling between sequence networks of a fully transposed transmis­sion holds also in 3-phase synchronous machines and 3-phase transformers. This fact leads to considerable simplications in the use of symmetrical components method in unsymmetrical fault analysis.

In case of three static unbalanced impedances, coupling appears between sequence networks and the method is no more helpful than a straight forward 3-phase analysis.