Methods of Circuit Analysis:
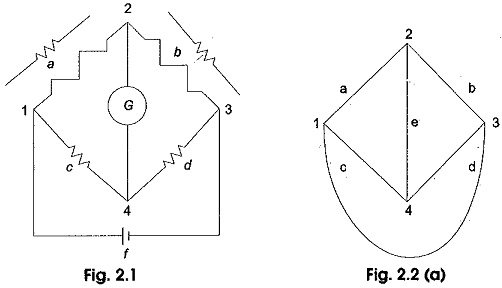
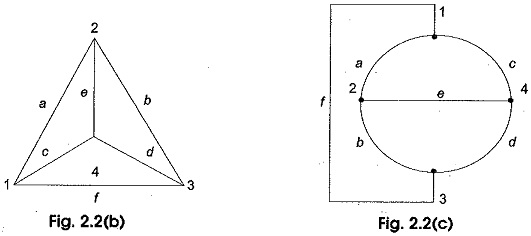
A division of mathematics called topology or graph theory deals with graphs of networks and provides information that helps in the formulation of network equations. In Methods of Circuit Analysis, all the elements in a network must satisfy Kirchhoff ‘s laws, besides their own characteristics. Based on these Circuit Analysis laws, we can form a number of equations. These Circuit Analysis equations can be easily written by converting the network into a graph. Certain aspects of network behaviour are brought into better perspective if a graph of the network is drawn. If each element or a branch of a network is represented on a diagram by a line irrespective of the characteristics of the elements, we get a graph. Hence, network topology is network geometry. A network is an interconnection of elements in various branches at different nodes as shown in Fig. 2.1. The corresponding graph is shown in Fig. 2.2 (a).
The graphs shown in Figs 2.2 (b) and (c) are also graphs of the network in Fig. 2.1.
It is interesting to note that the graphs shown in Fig. 2.2 (a), (b) and (c) may appear to be different but they are topologically equivalent. A branch is represented by a line segment connecting a pair of nodes in the graph of a network. A node is a terminal of a branch, which is represented by a point. Nodes are the end points of branches. All these graphs have identical relationships between branches and nodes.
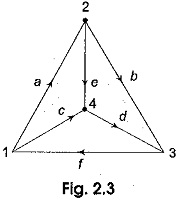
The three graphs in Fig. 2.2 have six branches and four nodes. These graphs are also called undirected. If every branch of a graph has a direction as shown in Fig. 2.3, then the graph is called a directed graph.
A node and a branch are incident if the node is a terminal of the branch. Nodes can be incident to one or more elements. The number of branches incident at a node of a graph indicates the degree of the node, For example, in Fig. 2.3 the degree of node 1 is three. Similarly, the degree of node 2 is three. If each element of the connected graph is assigned a direction as shown in Fig. 2.3 it is then said to be oriented. A graph is connected if and only if there is a path between every pair of nodes. A path is said to exist between any two nodes, for example 1 and 4 of the graph in Fig. 2.3, if it is possible to reach node 4 from node 1 by traversing along any of the branches of the graph. A graph can be drawn if there exists a path between any pair of nodes. A loop exists, if there is more than one path between two nodes.
Planar and Non–Planar Graphs
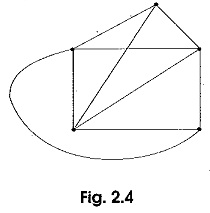
A graph is said to be planar if it can be drawn on a plane surface such that no two branches cross each other as shown in Fig. 2.2. On the other hand in a non-planar graph there will be branches which are not in the same plane as others, i.e. a non-planar graph cannot be drawn on a plane surface without a crossover. Figure 2.4 illustrates a non-planar graph.