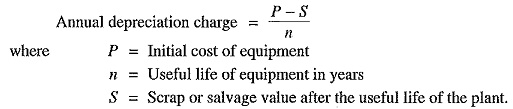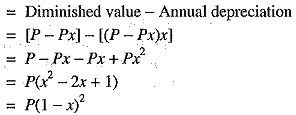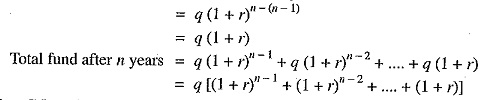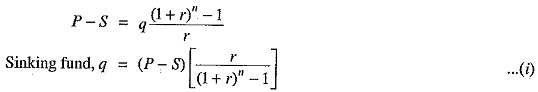Methods of Determining Depreciation:

There is reduction in the value of the equipment and other property of the plant every year due to depreciation. Therefore, a suitable amount (known as depreciation charge) must be set aside annually so that by the time the life span of the plant is over, the collected amount equals the cost of replacement of the plant.

The following are the commonly used methods for determining the annual depreciation charge:

• Straight line method ;
• Diminishing value method ;
• Sinking fund method.

(i) Straight line method. In this method, a constant depreciation charge is made every year on the basis of total depreciation and the useful life of the property. Obviously, annual depreciation charge will be equal to the total depreciation divided by the useful life of the property. Thus, if the initial cost of equipment is Rs 1,00,000 and its scrap value is Rs 10,000 after a useful life of 20 years, then,

In general, the annual depreciation charge on the straight line method may be expressed as :

The straight line method is extremely simple and is easy to apply as the annual depreciation charge can be readily calculated from the total depreciation and useful life of the equipment. Fig. 4.1 shows the graphical repre­sentation of the method. It is clear that initial value P of the equipment reduces uniformly, through depreciation, to the scrap value S in the useful life of the equipment. The depreciation curve (PA) follows a straight line path, indicating constant annual depreciation charge. However, this method suffers from two defects. Firstly, the assumption of constant depreciation charge every year is not correct. Secondly, it does not account for the interest which may be drawn during accumulation.

(ii) Diminishing value method. In this method, depreciation charge is made every year at a fixed rate on the diminished value of the equipment. In other words, depreciation charge is first appf ed to the initial cost of equipment and then to its diminished value. As an example, suppose the initial cost of equipment is Rs 10,000 and its scrap value after the useful life is zero. If the annual rate of depreciation is 10%, then depreciation charge for the first year will be 0.1 x 10,000 = Rs 1,000. The value of the equipment is diminished by Rs 1,000 and becomes Rs 9,000. For the second year, the depreciation charge will be made on the diminished value (i.e. Rs 9,000) and becomes 0.1 x 9,000 = Rs 900. The value of the equipment now becomes 9000 — 900 = Rs 8100. For the third year, the depreciation charge will be 0.1 x 8100 = Rs 810 and so on.

Mathematical treatment

Let

P = Capital cost of equipment

n= Useful life of equipment in years

S = Scrap value after useful life

Suppose the annual unit depreciation is x. It is desired to find the value of x in terms of P, n and S.

Value of equipment after one year

Value of equipment after 2 years

Value of equipment after n years

But the value of equipment after n years (i.e., useful life) is equal to the scrap value S.

From exp. (i), the annual depreciation can be easily found. Thus depreciation to be made for the first year is given by

Similarly, annual depreciation charge for the subsequent years can be calculated.

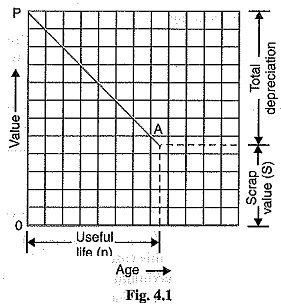
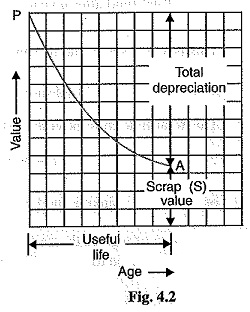
This method is more rational than the straight line method. Fig. 4.2 shows the graphical representation of diminishing value method. The initial value P of the equipment reduces, through depreciation, to the scrap value S over the useful life of the equipment. The depreciation curve follows the path PA. It is clear from the curve that depreciation charges are heavy in the early years but decrease to a low value in the later years. This method has two drawbacks. Firstly, low depreciation charges are made in the late years when the maintenance and repair charges are quite heavy. Secondly, the depreciation charge is independent of the rate of interest which it may draw during accumulation. Such interest moneys, if earned, are to be treated as income.

(iii) Sinking fund method. In this method, a fixed depreciation charge is made every year and interest compounded on it annually. The constant depreciation charge is such that total of annual instalments plus the interest accumulations equal to the cost of replacement of equipment after its useful life.

Let us suppose that an amount of q is set aside as depreciation charge every year and interest compounded on it so that an amount of P – S is available after n years. An amount q at annual interest rate of r will become *q(1 + r)ⁿ at the end of n years.

Now, the amount q deposited at the end of first year will earn compound interest for n -1 years and shall become q(1+r)^n-1 i.e.,

Amount q deposited at the end of first year becomes

Amount q deposited at the end of 2nd year becomes

Amount q deposited at the end of 3rd year becomes

Similarly amount q deposited at the end of n – 1 year becomes

This is a G.P. series and its sum is given by :

This total fund must be equal to the cost of replacement of equipment i.e., P – S.

The value of q gives the uniform annual depreciation charge. The paraenthetical term in eq. (i) is frequently referred to as the “sinking fund factor”.

Though this method does not find very frequent application in practical depreciation accounting, it is the fundamental method in making economy studies.

High Load Factor:

The load factor plays a vital role in determining the cost of energy. Some important advantages of high load factor are listed below :

• Reduces cost per unit generated : A high load factor reduces the overall cost per unit The higher the load factor, the lower is the generation cost. It is because higher load factor means that for a given maximum demand, the number of units generated is more. This reduces the cost of generation.
• Reduces variable load problems : A high load factor reduces the variable load problems on the power station. A higher load factor means comparatively less variations in the load demands at various times. This avoids the frequent use of regulating devices installed to meet the variable load on the station.