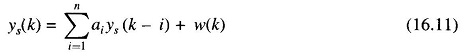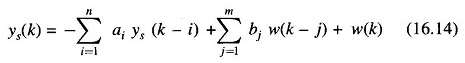Time Series Forecasting Methods:
If yd(k) is subtracted from the sequence y(k), the result would be a sequence of data for the stochastic part of the load. We have to identify the model for ys(k) and then use it to make the prediction ys(k + j). A convenient method for this is based on the use of the stochastic time series forecasting methods. The simplest form of such a model is the so called auto-regressive model which has been widely used to represent the behavior of a zero mean stationary stochastic sequence. The method proposed for the generation of data for ys(k) ensures that the sequence ys(k) will have a zero mean. If it is also assumed to be stationary, it may be possible to identify a suitable autoregressive model for this sequence.
Auto-regressive Models:
The sequence ys(k) is said to satisfy an AR model of order n i.e. it is [AR(n)], if it can be expressed as
where ai are the model parameters and w(k) is a zero mean white sequence. In order that the solution of this equation may represent a stationary process, it is required that the coefficients ai make the roots of the characteristics equation
lie inside the unit circle in the z-plane.
The problem in estimating the value of n is referred to as the problem of structural identification, while the problem of estimation of the parameters ai is referred to as the problem of parameter estimation. An advantage of the AR model is that both these problems are solved relatively easily if the autocorrelation functions are first computed using the given data. Once the model order n and the parameter vector a have been estimated, the next problem is that of estimating the statistics of the noise process w(k). The best that can be done, is based on the assumption that an estimate of w(k) is provided by the residual e(k) = ys(k) — ŷs(k), the estimate ŷs(k) having been determined from
The variance σ2 of w(k) is then estimated using the relation
Auto-Regressive Moving-Average Models:
In some cases, the AR model may not be adequate to represent the observed load behavior unless the order n of the model is made very high. In such a case ARMA (n, m) model is used.
Estimation of two structural parameters n and m as well as model parameters ai, bj and the variance σ2 of the noise term w(k) is required. More complex behavior can be represented. The identification problem is solved off-line. The acceptable load model is then utilized on-line for obtaining on-line load forecasts. ARMA model can easily be modified to incorporate the temperature, rainfall, wind velocity and humidity data. In some cases, it is desirable to show the dependence of the load demand on the weather variables in an explicit manner. The time series forecasting methods are easily generalized in order to reflect the dependence of the load demand on one or more of the weather variables.