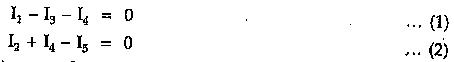Nodal analysis:

This Nodal analysis method is mainly based on Kirchhoff’s Current Law (KCL). This method uses the analysis of the different nodes of the network. We have already defined a node. Every junction point in a network, where two or more branches meet is called a node. One of the nodes is assumed as reference node whose potential is assumed to be zero. It is also called zero potential node or datum node. At other nodes the different voltages are to be measured with respect to this reference node. The reference node should be given a number zero and then the equations are to be written for all other nodes by applying KCL. The advantage of this method lies in the fact that we get (n – 1) equations to solve if there are ‘n’ nodes. This reduces calculation work.

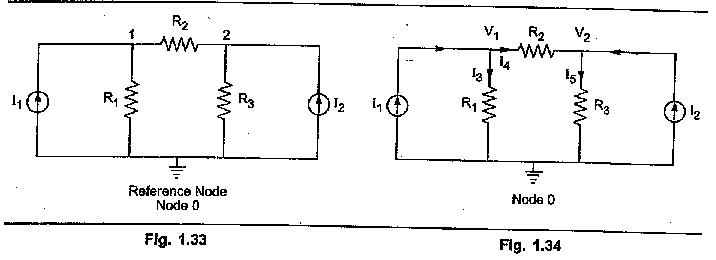
Consider the following network shown in the Fig. 1.33.

Let voltages at node 1 and node 2 be V₁ and V₂. Mark various branch currents as shown in the Fig. 1.34. Now analyse each node using KCL independently.

Now applying KCL at node 1,

The currents in these equations can be expressed interms of node voltages as,

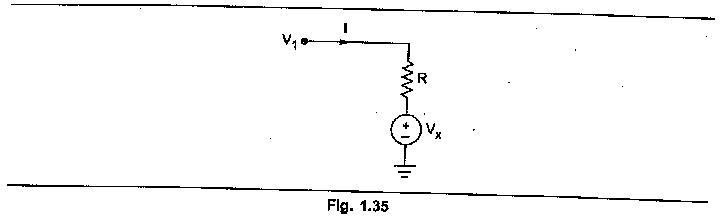
As I₁ and I₂ are known, we get two equations (3) and (4) with the two unknowns V₁ and V₂. Solving these equations simultaneously, the node voltages V₁ and V₂ can be determined. Once V₁ and V₂ are known, current through any branch of the network can be determined. If there exists a voltage source in any of the branches as shown in the Fig. 135 then that must be considered while writing the equation for the current through that branch.

Now V₁ is at higher potential with respect to base, forcing current I downwards. While polarity of V_x is such that it tries to force current upwards. So in such a case equation of current becomes,

If the direction of current I is assumed entering the node then it is assumed that V_x is more than V₁ and hence equation for current I becomes,

Similarly if the polarities of voltage source is opposite then it helps the node voltage and appears with positive sign in the equations.

Points to Remember for Nodal Analysis

1. While assuming branch currents, make sure that each unknown branch current is considered at least once.
2. Convert the voltage source present into their equivalent current sources for node analysis, wherever possible.
3. Follow the same sign convention, currents entering at node are to be considered positive, while currents leaving the node are to be considered as
4. As far as possible, select the directions of various branch currents leaving the respective nodes.