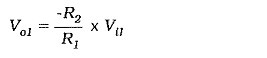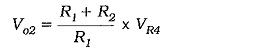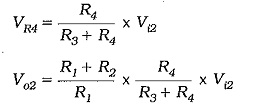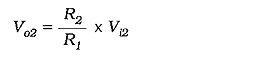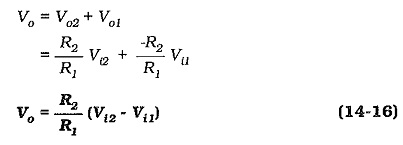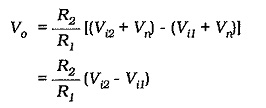Differential Amplifier Circuit Operation:

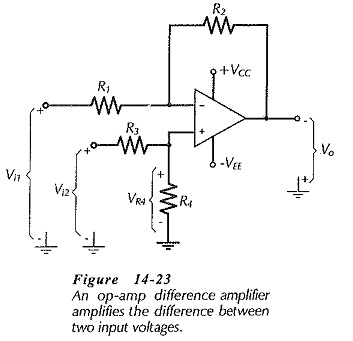
A Differential Amplifier Circuit Operation amplifies the difference between two inputs. The circuit shown in Fig. 14-23 is a combination of inverting and noninverting amplifiers. Resistors R₁, R₂, and the op-amp constitutes an inverting amplifier for a voltage (V_i1) applied to R₁. The same components (R₁, R₂, and the op-amp) also function as a noninverting amplifier for a voltage (V_R4) at the noninverting input terminal. It is seen that V_R4 is derived from input voltage V_i2 by the voltage divider R₃ and R₄.

To understand the Differential Amplifier Circuit Operation, consider the output produced by each input voltage when the other input is zero:

with V_i2 = 0,

with V_i1 = 0,

and

with R₃ = R₁, and R₄ = R₂,

When both inputs are present,

When R₂ = R₁, the output voltage (as calculated by Eq. 14-16) is the direct difference between the two inputs. With R₂ greater than R₁, the output becomes an amplifier version of (V_i2 – V_i1).

Input resistances:

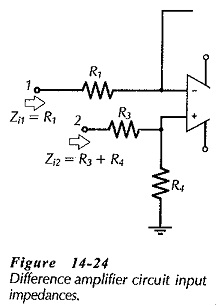
Consider the input portion of the Differential Amplifier Circuit Operation reproduced in Fig. 14-24. The resistance at input terminal 1 is the same as the input impedance for an inverting amplifier: Z_i1 = R₁. The input resistance at the op-amp noninverting input terminal, is very high (as in the case of a noninverting amplifier), and this is in parallel with resistor R₄. So, the input impedance at terminal 2 in Fig. 14-24 is Z_i2 = R₃ + R₄.

Equation 14-16 was derived by assuming that R₃ = R₁, and R₄ = R₂. It can be shown that the same result is obtained when the ratio R₄/R₃ equals R₂/R₁, so that the actual resistor values do not have to be equal For equal resistances at the two input terminals

Then, calculate the resistances of R₃ and R₄ from,

A simple rule-of-thumb can be used for determining suitable resistance values for R₃ and R₄ when the two input resistances do not have to be exactly equal. Select, R₄ = R₂/A_CL; which always makes R₄ = R₁. Then, calculate R₃ as, R₃ = R₁/A_CL.

Common Mode Voltages:

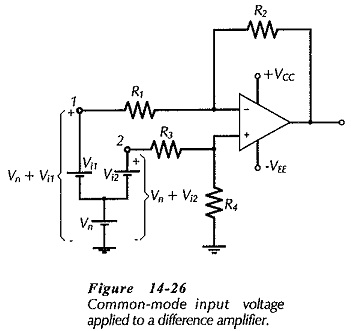
A common-mode input voltage is a signal voltage (dc or ac) applied to both input terminals at the same time. This is illustrated in Fig. 14-26, where V_i1, V_i2, and the common-mode voltage (V_n) are all represented as inputs from dc sources. As shown, the input voltages at terminals 1 and 2 are changed from V_i1 and V_i2 to (V_n + V_i1) and (V_n + V_i2).

Equation 14-16 shows that the output voltage is the amplified difference between the two input voltages. So,

This shows that the common-mode input is completely cancelled. However, recall that the gain equation depends upon the resistor ratios (R₄/R₃ and R₂/R₁) being equal If the ratios are not exactly equal, one input will experience a larger amplification than the other. Also, the common-mode voltage at one input terminal will be amplified by a larger amount than that applied to the other input terminal. In this case, common-mode inputs will not be completely cancelled.

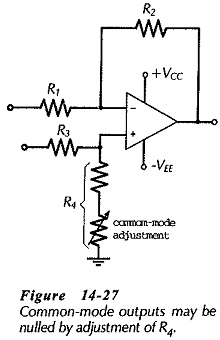
Because it is difficult to perfectly match resistor ratios (especially for standard-value components), some common-mode output voltage is almost certain to be produced where a common-mode input exists. Figure 14-27 shows a circuit modification for minimizing common-mode outputs from a difference amplifier. Resistor R₄ is made up of a fixed-value resistor and a small-value adjustable resistor connected in series. This provides adjustment of the ratio R₄/R₃ to match R₂/R₁, so that common-mode outputs can be nulled to zero.