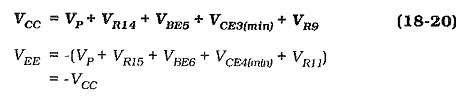BJT Power Amplifier with Differential Input Stages:

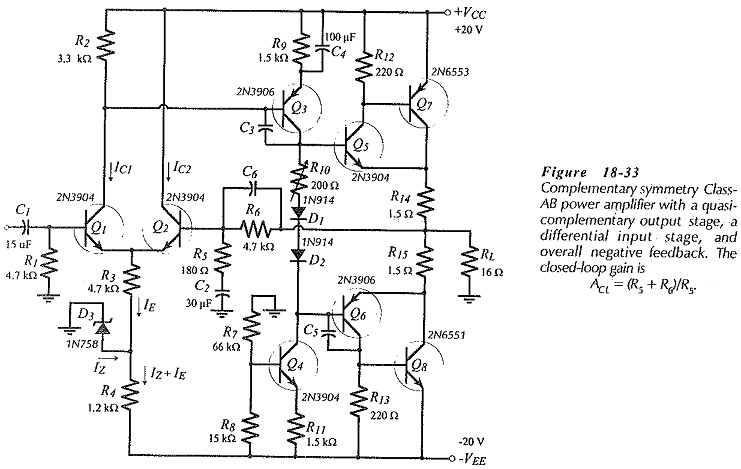
Amplifier Circuit – The direct-coupled amplifier in Fig. 18-33 has a BJT Power Amplifier with Differential Input Stages constituted by transistors Q₁ and Q₂. It also has an intermediate stage (Q₃) with a constant current load (Q₄). Both pairs of output stage transistors (Q₅ and Q₇) and (Q₆ and Q₈) are in quasi-complementary configuration, instead of the usual complementary form. This arrangement helps to minimize the required supply voltage by removing the V_BE of the power transistors from the V_CC equation.

The BJT Power Amplifier with Differential Input Stages facilitates negative feedback (NFB), and the whole circuit functions like an operation amplifier. Q₁ base is the noninverting input, Q₂ base is the inverting input, and the junction of R₁₄ and R₁₅ is the output terminal. There is 100% dc NFB provided from the output via R₆ to Q₂ base. This keeps the output dc voltage at the same level as Q₁ base, (at ground). With C₂ behaving as an ac short-circuit, the ac NFB is divided by R₅ and R₆ to give a closed loop gain; A_CL = (R₅ + R₆)/R₅.

Zener diode D₃ and resistor R₄ decouple the power supply ripple on the negative supply line. The dynamic impedance of D₁ combined with R₄ functions as an ac voltage divider to attenuate the ripple at the emitters of Q₁ and Q₂. Ripple at this point is amplified just like an input signal. Capacitors C₃ and C₅ are frequency-compensating components.

Amplifier Design:

The design procedure for the output and intermediate stages of the circuit in Fig. 18-33 is similar to procedures already discussed. Design of the BJT Power Amplifier with Differential Input Stages is very simple. The dc collector currents for Q₁ and Q₂ should be larger than the peak base current for Q₃, and the voltage drop across R₂ is (V_E3 + V_BE3). Zener voltage V_Z3 is any convenient level, usually around 0.5 V_EE. Resistor R₃ is calculated to pass I_E ≈ (I_C1 + I_C2), and R₄ must pass (I_Z + I_E).

Q₁ bias resistor R₁ is determined from earlier Equation, R₆ is selected equal to R₁, and R₅ is calculated in terms of R₆ to give the desired closed-loop gain. The impedance of C₂ is made equal to R₅ at the desired lower cutoff frequency (f₁), so that C₂ sets f₁. Capacitors C₁ and C₄ are determined in the usual way for capacitors that are not to affect f₁. An additional capacitor (C₆) might be included to set the upper cutoff frequency (f₂); (X_C6 = R₆ at f₂).