Exponential Variation of the Input to the Controller:
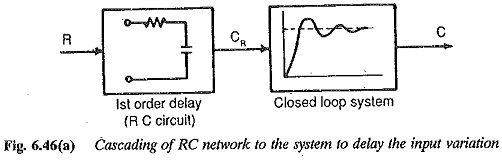
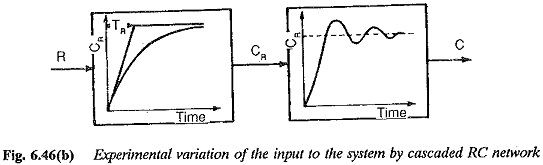
The linear Exponential Variation of the input to the Controller, discussed in the foregoing section, is too involved to achieve by means of circuits using discrete elements. On the other hand a simple RC circuit connected at the input of the controller provides an input which varies exponentially. This RC circuit functions as a limiter having a time constant Tc. The cascading of this with the modified system designed using the above criteria is shown in Fig. 6.46 by a block diagram
The closed loop transfer function of the total system is
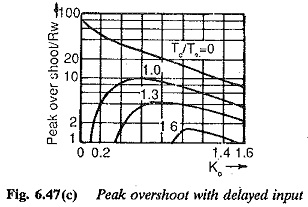
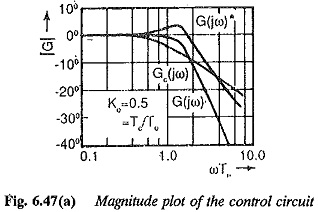
The magnitude plots of this function drawn for a given value of K0 and different value of Tc are shown in Fig. 6.47(a). For comparison, the plot for RC = 0 is also shown which corresponds to a step input. The value of K0 is chosen to provide a lightly damped system. So, the magnitude plot shows a resonant peak which is representative of overshoot in the transient response. As Tc > 0 the resonant peak disappears and the slope beyond the corner frequency increases. The time response is similar to that having increased damping. The time responses of the system for different Tc, shown in Fig. 6.47(b), support the conclusion. The overshoot as a function of K0, Tc being the parameter is depicted in Fig. 6.47(c). The offer helping tools in the suitable choice of Tc for given K0 or vice versa. For a K0 of 0.8 the value of Tc can be in the range of 1.6 to 1.3.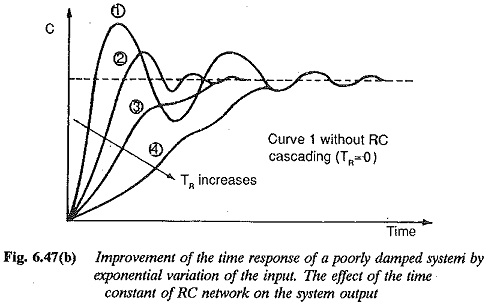
Hence from the above discussion it may be concluded that the transient behaviour of a lightly damped system can be improved by having a Exponential Variation in the input to the system. The variation can be linear or Exponential Variation. The latter is easier to realise with simple RC circuits. The time of variation of the input quantity, as decided by the limiter in the former and by the time constant Tc in the latter, influence the transient response very much.