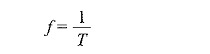The Sine Wave:

Many a time, alternating voltages and currents are represented by a sinusoidal wave, or simply a sinusoid. It is a very common type of alternating, current (ac) and alternating voltage. The sinusoidal wave is generally referred to as a sine wave. Basically an alternating voltage (current) waveform is defined as the voltage (current) that fluctuates with time periodically, with change in polarity and direction.

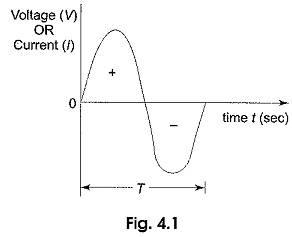
In general, the sine wave is more useful than other waveforms, like pulse, sawtooth, square, etc. There are a number of reasons for this. One of the reasons is that if we take any second order system, the response of this system is a sinusoid. Secondly, any periodic waveform can be written in terms of sinusoidal function according to Fourier theorem. Another reason is that its derivatives and integrals are also sinusoids. A sinusoidal function is easy to analyse. Lastly, the sinusoidal function is easy to generate, and it is more useful in the power industry. The shape of a sinusoidal waveform is shown in Fig. 4.1.

The waveform may be either a current waveform, or a voltage waveform. As seen from the Fig. 4.1, the wave changes its magnitude and direction with time. If we start at time t= 0, the wave goes to a maximum value and returns to zero, and then decreases to a negative maximum value before returning to zero. The sine wave changes with time in an orderly manner. During the positive portion of voltage, the current flows in one direction; and during the negative portion of voltage, the current flows in the opposite direction. The complete positive and negative portion of the wave is one cycle of the sine wave. Time is designated by t. The time taken for any wave to complete one full cycle is called the period (T).

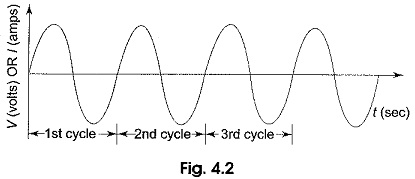
In general, any periodic wave constitutes a number of such cycles. For example, one cycle of a sine wave repeats a number of times as shown in Fig. 4.2. Mathematically it can be represented as f(t) = f(t + T) for any t.

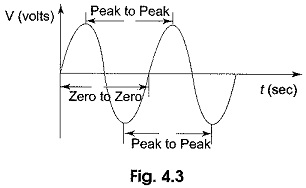
The period can be measured in the following different ways (See Fig. 4.3).

• From zero crossing of one cycle to zero crossing of the next cycle.
• From positive peak of one cycle to positive peak of the next cycle, and 
• From negative peak of one cycle to negative peak of the next cycle.

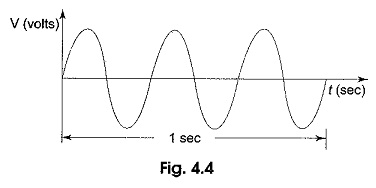
The frequency of a wave is defined as the number of cycles that a wave completes in one second.

In Fig. 4.4 the sine wave completes three cycles in one second. Frequency is measured in hertz. One hertz is equivalent to one cycle per second, 60 hertz is 60 cycles per second and so on. In Fig. 4.4, the frequency denoted by f is 3 Hz, that is three cycles per second. The relation between time period and frequency is given by

A sine wave with a longer period consists of fewer cycles than one with a shorter period.