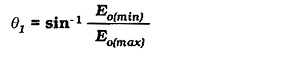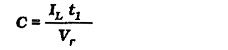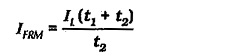Full Wave Rectifier DC Power Supply:

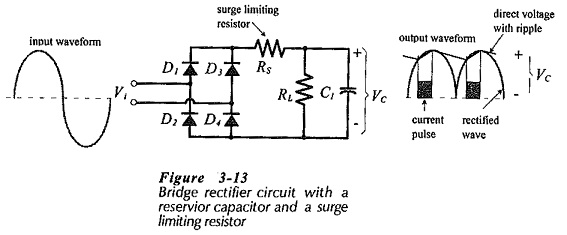
Like half-wave rectifiers, full-wave rectifiers require filter circuits to convert the output waveform to direct voltage. Figure 3-13 shows a Full Wave Rectifier DC Power Supply with a reservior capacitor and a surge limiting resistor. These components operate exactly as explained for the half-wave rectifier circuit, with a few important exceptions.

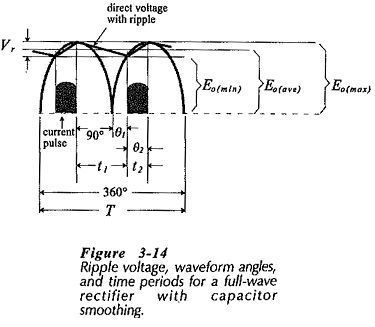
The capacitor-smoothed full-wave rectifier waveforms are shown in detail in Fig. 3-14. Equation 3-7, derived for the half-wave rectifier circuit, still applies for determining the angle θ₁.

Eq. 3-7,

Also, θ₂ can be determined from Eq.3-8,

Eq. 3-8,

and Eq. 3-9 can be used for time t₂

Eq. 3-9

Comparing Fig. 3-14 and Fig. 3-8, it is seen that the capacitor discharge time (t₁) for the half-wave circuit is approximately equal to the waveform time period (T), whereas for the full-wave circuit t₁ approximately equals T/2. More precisely,

Using the correct value of t₁, Eq. 3-11 can be used for calculating the reservior capacitance for a full-wave rectifier circuit.

Eq. 3-11,

Similarly, (using the correct value of t₁ in Fig. 3-14), the repetitive current (I_FRM) can be determined from Eq. 3-15,

Eq. 3-15,

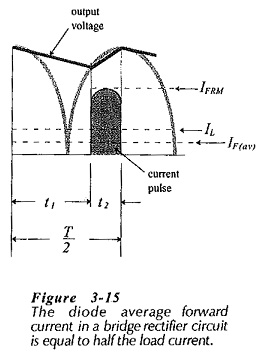
The average forward current passed by the bridge rectifier circuit is equal to the load current. But, each pair of diodes supplies current for no more than a half cycle of the input wave. The other pair conducts during the other half cycle. So, as illustrated in Fig. 3-15, the diode average forward current is half of the load current.

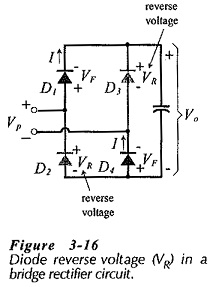
Another difference between the half-wave and full-wave rectifier power supply circuits concerns the reverse voltage applied to the diodes. Consider Fig. 3-16. When the instantaneous input voltage is +V_p, as illustrated, V_p is applied across forward-biased diode D₁ in series with reverse-biased diode D₃. Therefore, the reverse voltage across D₃ is,

Examination of the circuit shows that Eq. 3-18 applies to each diode when reverse biased.

As in the case of the half-wave circuit, the capacitor calculation can be simplified by assuming that time t₂ is very much smaller than t₁. This gives the approximation that the capacitor discharge time is equal to half the input waveform time period.