Light Wave Spectrum:
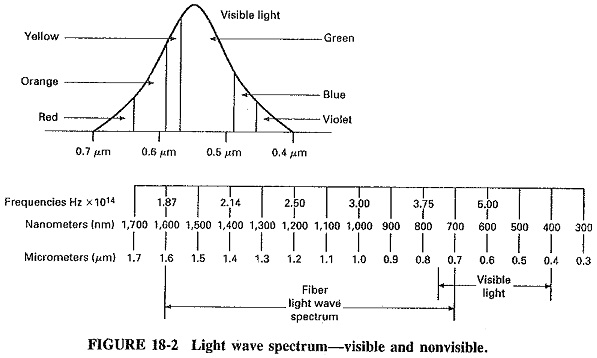
Light Wave Spectrum – In everyday terms, light can be defined as the pail of the visible spectrum that has a wavelength range between 0.4 μm (micrometer) and 0.7 μm (refer to Figure 18-2 to locate the color spectrum). This definition must be broadened somewhat for use in the optical (guided-light) communications field because of the variety of light sources used to transmit this information (700 to 1600 nm).
Wavelengths of Light Wave Spectrum are extremely short. Their distances are measured in units called angstroms, after the Swedish physicist Anders J. Angstrom. A single angstrom is 1 ten-billionth of a meter. In the fiber industry, the terms used more frequently to measure wavelengths of light are the micrometer and the nanometer. Since all Light Wave Spectrum travel at the same speed in air or in a vacuum, and since each color has a different wavelength, it may be assumed that each color has a discrete frequency.
Reflection and Refraction:
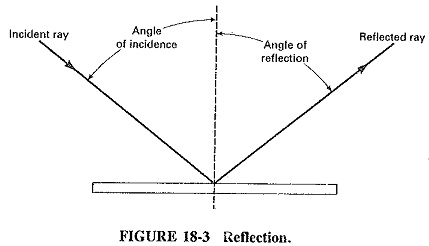
We are all familiar with light that is reflected from a flat, smooth surface such as a mirror. These reflections (see Figure 18-3) are the result of an incident ray and the reflected ray. The angle of reflection is determined by the angle of incidence.
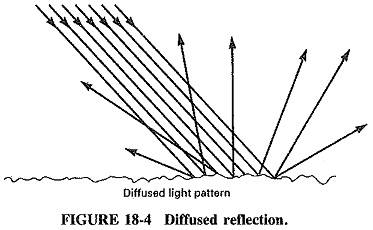
Reflections in many directions are called diffuse reflection and are the result of Light Wave Spectrum being reflected by an irregular surface (see Figure 18-4). The result of this process can be easily illustrated by using the page you are now reading as an example. White light, which includes all colors, is reflected by the rough surface of this page because the roughness is random. The reflected light is random (that is, it reflects in all directions), and because the paper does not absorb much of the light, the light seems to radiate equally from all parts of the page.
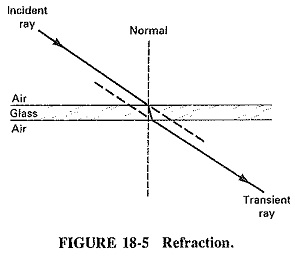
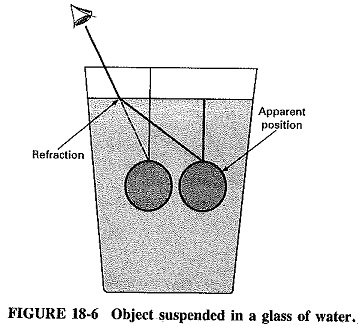
Another property of light is refraction. This is caused by a change in the speed of light as it passes through different mediums such as air, water, glass, and other transparent substances (see Figure 18-5). This phenomenon is commonly evident when objects are viewed through a glass of water, for example (see Figure 18-6). The refractive index can be stated as:
where
c = velocity of light in space
ν = velocity of light in specific material
Each transparent substance has its own refractive index number (see Table 18-1).
Dispersion, Diffraction, Absorption, and Scattering:
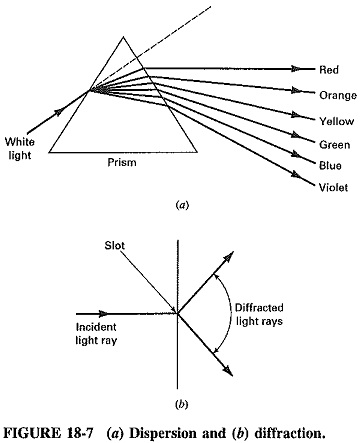
Dispersion is the process of separating light into each of its component frequencies. It is commonly recognizable when sunlight is dispersed into a rainbow of colors by a prism (see Figure 18-7a).
Diffraction is the bending of light as it passes through an opening in an obstacle (see Figure 18-7b).
Absorption takes place when light strikes a surface (flat black) and is converted into heat through an exchange of energy with the atoms of the surface; in this case there is little or no reflection.
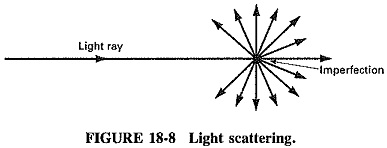
Scattering occurs when light strikes a substance which in turn emits light of its own at the same wavelength as the incident light (see Figure 18-8). If the substance emits light of a wavelength longer than that of the incident light, this is called luminescence. Examples of luminescence are watch dials that glow in the dark because of the absorption of light during the day and the emission of Light Wave Spectrum (as the atoms return to their normal state) at night. The amount of energy contained in light is determined to some extent by wavelength or frequency. As an example, ultraviolet light has 100 times the energy level as red visible light. The energy in a photon (a particle of light) can be calculated by Equation (18-2).
where
h = 6.63 x 10-34 (Planck’s constant)
f = frequency (wavelength)
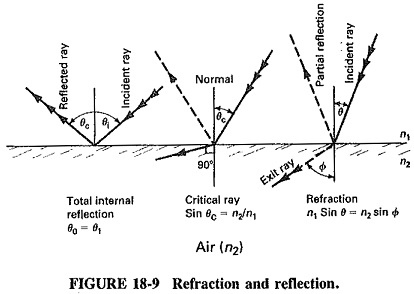
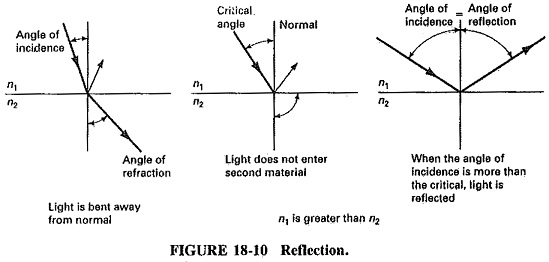
The angle of refraction of Light Wave Spectrum traveling from one medium to another depends on the index of the two media (see Table 18-1). As shown in Figure 18-9, the vertical line, which is referred to as the normal, is an imaginary line perpendicular to the junction between the two media. The angle of incidence is the angle between the incident ray and the normal. The angle of refraction is the angle between the refracted ray and the normal.
Light passing from a lower refractive index (as shown in Figure 18-10) to a higher one is bent toward the normal, and vice versa. If the angle of incidence moves away from the normal to a point 90° from it, it is called the critical angle. At this point, light has gone from the refractive mode to the reflective mode.
Independent of the index of the two media, a small portion of light will always be reflected when light passes from one index to another, this is called Fresnel reflection (p) and can be calculated by using Equation (18-3).
where
p = the boundary between air and some other material,
The importance of this equation becomes apparent when we relate this information to Equation (18-4).
We can establish fiber losses in decibels by understanding these two relationships (the average loss in a fiber splice is 0.15 dB).
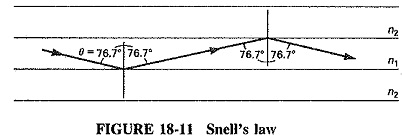
When light passes through fiber, another situation, which is governed by Snell’s law, arises. This law states the relationship between the incident and refracted rays as Equation (18-5).
This law shows that the angles depend on the refractive indices of the two materials.
The critical angle of incidence θc1, where θ2 = 90°, is:
Light striking the boundary of n1 and n2 at an angle greater than 76.7° will be reflected back to its source at that same angle (see Figure 18-11).