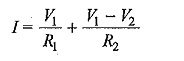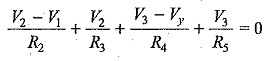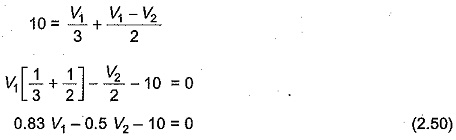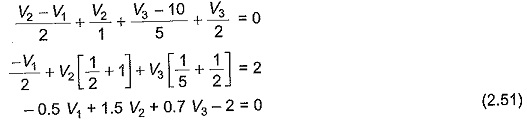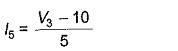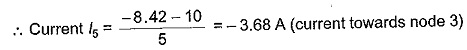Supernode Analysis:
Suppose any of the branches in the network has a voltage source, then it is slightly difficult to apply nodal analysis. One way to overcome this difficulty is to apply the Supernode Analysis. In this method, the two adjacent nodes that are connected by a voltage source are reduced to a single node and then the equations are formed by applying Kirchhoff s current law as usual. This is explained with the help of Fig. 2.44.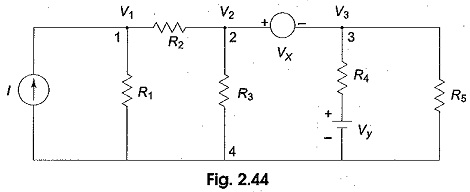
It is clear from Fig. 2.44, that node 4 is the reference node. Applying Kirchhoff s current law at node 1, we get
Due to the presence of voltage source Vx in between nodes 2 and 3, it is slightly difficult to find out the current. The supernode technique can be conveniently applied in this case.
Accordingly, we can write the combined equation for nodes 2 and 3 as under.
From the above three equations, we can find the three unknown voltages.
Examples:
Determine the current in the 5 Ω resistor for the circuit shown in Fig. 2.45.
Solution At node 1
At node 2 and 3, the supernode equation is
The voltage between nodes 2 and 3 is given by
The current in the 5 Ω resistor
Solving Eqs 2.50, 2.51 and 2.52, we obtain
i.e. the current flows towards node 3.