Four Quadrant Operation of Motor Drive:
For consideration of Four Quadrant Operation of Motor Drive, it is useful to establish suitable conventions about the signs of torque and speed. Motor speed is considered positive when rotating in the forward direction. For drives which operate only in one direction, forward speed will be their normal speed. In loads involving up-and-down motions, the speed of motor which causes upward motion is considered forward motion. For reversible drives, forward speed is chosen arbitrarily. Then the rotation in opposite direction gives reverse speed which is assigned the negative sign. Positive motor torque is defined as the torque which produces acceleration or the positive rate of change of speed in forward direction. According to Eq. (2.2), positive load torque is opposite in direction to the Positive motor torque. Motor torque is considered negative if it produces deceleration.![]()
A motor operates in two modes motoring and braking. In motoring, it converts electrical energy to mechanical energy, which supports its motion. In braking, it works as a generator converting mechanical energy to electrical energy, and thus, opposes the motion. Motor can provide motoring and braking operations for both forward and reverse directions.
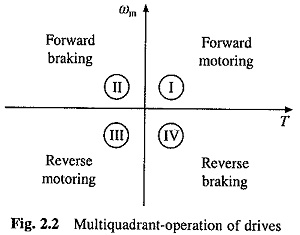
Figure 2.2 shows the torque and speed coordinates for both forward (positive) and reverse (negative) motions of Four Quadrant Operation of Motor Drive. Power developed by a motor is given by the product of speed and torque. In quadrant I, developed power is positive. Hence, machine works as a motor supplying mechanical energy. Operation in quadrant I is, therefore, called forward motoring. In quadrant II, power is negative. Hence, machine works under braking opposing the motion. Therefore, operation in quadrant II is known as forward braking. Similarly, operations in quadrant III and IV can be identified as reverse motoring and braking respectively.
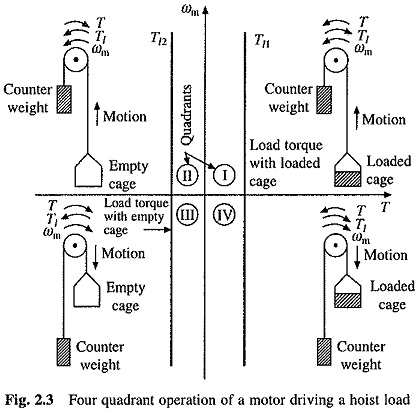
For better understanding of the above notations, let us consider operation of a hoist in Four Quadrant Operation of Motor Drive as shown in Fig. 2.3. Directions of motor and load torques, and direction of speed are marked by arrows.
A hoist consists of a rope wound on a drum coupled to the motor shaft. One end of the rope is tied to a cage which is used to transport man or material form one level to another level. Other end of the rope has a counter weight. Weight of the counter weight is chosen to be higher than the weight of an empty cage but lower than of a fully loaded cage.
Forward direction of motor speed will be one which gives upward motion of the cage. Speed-torque characteristics of the hoist load are also shown in Fig. 2.3. Though the positive load torque is opposite in sign to the positive motor torque, according to Eq. (2.2), it is convenient to plot it on the same axes. Load-torque curve drawn in this manner is, in fact, negative of the actual.
Load torque has been shown to be constant and independent of speed. This is nearly true with a low speed hoist where forces due to friction and windage can be considered to be negligible compared to those due to gravity. Gravitational torque does not change its sign even when the direction of driving motor is reversed. Load torque line Tl1 in quadrants I and IV represents speed-torque characteristic for the loaded hoist. This torque is the difference of torques due to loaded hoist and counter weight. The load torque line Tl2 in quadrants II and III is the speed-torque characteristic for an empty hoist. This torque is the difference of torques due to counter weight and the empty hoist. Its sign is negative because the weight of a counter weight is always higher than that of an empty cage.
The quadrant I operation of a hoist requires the movement of the cage upward, which corresponds to the positive motor speed which is in anticlockwise direction here. This motion will be obtained if the motor produces positive torque in anticlockwise direction equal to the magnitude of load torque Tl1. Since developed motor power is positive, this is forward motoring operation.
Quadrant IV operation is obtained when a loaded cage is lowered. Since the weight of a loaded cage is higher than that of a counter weight, it is able to come down due to the gravity itself. In order to limit the speed of cage within a safe value, motor must produce a positive torque T equal to Tl2 in anticlockwise direction. As both power and speed are negative, drive is operating in reverse braking.
Operation in quadrant II is obtained when an empty cage is moved up. Since a counter weight is heavier than an empty cage, it is able to pull it up. In order to limit the speed within a safe value, motor must produce a braking torque equal to Tl2 in clockwise (negative) direction. Since speed is positive and developed power negative, it is forward braking operation.
Operation in quadrant III is obtained when an empty cage is lowered. Since an empty cage has a lesser weight than a counter weight, the motor should produce a torque in clockwise direction. Since speed is negative and developed power positive, this is reverse motoring operation.