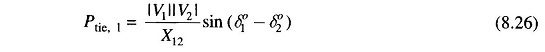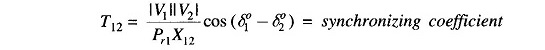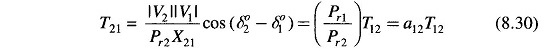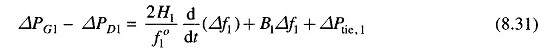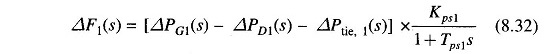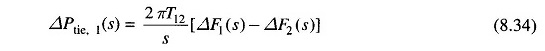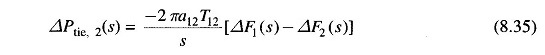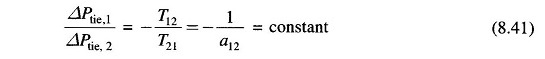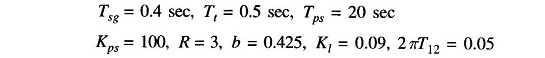Two Area Load Frequency Control:

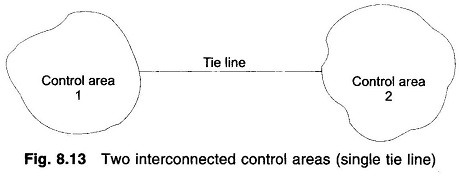
Two Area Load Frequency Control – An extended power system can be divided into a number of Two Area Load Frequency Control areas interconnected by means of tie lines. Without loss of generality we shall consider a two-area case connected by a single tie line as illustrated in Fig. 8.13.

The control objective now is to regulate the frequency of each area and to simultaneously regulate the tie line power as per inter-area power contracts. As in the case of frequency, proportional plus integral controller will be installed so as to give zero steady state error in tie line power flow as compared to the contracted power.

It is conveniently assumed that each control area can be represented by an equivalent turbine, generator and governor system. Symbols used with suffix 1 refer to area 1 and those with suffix 2 refer to area 2.

In an isolated control area case the incremental power (ΔP_G – ΔP_D) was accounted for by the rate of increase of stored kinetic energy and increase in area load caused by increase in frequency. Since a tie line transports power in or out of an area, this fact must be accounted for in the incremental power balance equation of each area.

Power transported out of area 1 is given by

where

δ⁰₁,δ⁰₂ = power angles of equivalent machines of the two areas.

For incremental changes in δ₁ and δ₂, the incremental tie line power can be expressed as

Where

Since incremental power angles are integrals of incremental frequencies, we can write Eq. (8.27) as

where Δf₁ and Δf₂ are incremental frequency changes of areas 1 and 2, respectively.

Similarly the incremental tie line power out of area 2 is given by

Where

With reference to earlier equation, the incremental power balance equation for area 1 can be written as

It may be noted that all quantities other than frequency are in per unit in Eq. (8.31).

Taking the Laplace transform of Eq. (8.31) and reorganizing, we get

where as defined earlier

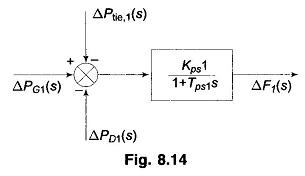
Compared to earlier equation of the isolated control area case, the only change is the appearance of the signal ΔP_tie,1(s) as shown in Fig. 8.14.

Taking the Laplace transform of Eq. (8.28), the signal ΔP_tie,1(s) is obtained as

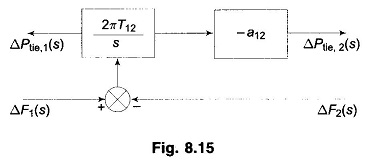
The corresponding block diagram is shown in Fig. 8.15.

For the control area 2, ΔP_tie,2(s) is given by [Eq. (8.29)]

which is also indicated by the block diagram of Fig. 8.15.

Let us now turn our attention to ACE (area control error) in the presence of a tie line. In the case of an isolated control area, ACE is the change in area frequency which when used in integral control loop forced the steady state frequency error to zero. In order that the steady state tie line power error in a two-area control be made zero another integral control loop (one for each area) must be introduced to integrate the incremental tie line power signal and feed it back to the speed changer. This is accomplished by a single integrating block by redefining ACE as a linear combination of incremental frequency and tie line power. Thus, for control area 1

where the constant b₁ is called area frequency bias.

Equation (8.36) can be expressed in the Laplace transform as

Similarly, for the control are a 2, ACE₂ is expressed as

Combining the basic block diagrams of the two control areas, with ΔP_C1(s) and ΔP_C2(s) generated by integrals of respective ACEs (obtained through signals representing changes in tie line power and local frequency bias) and employing the block diagrams of Figs. 8.14 to 8.15, we easily obtain the composite block diagram of Fig. 8.16.

Let the step changes in loads ΔP_D1 and ΔP_D2 be simultaneously applied in control areas 1 and 2, respectively. When steady conditions are reached, the output signals of all integrating blocks will become constant and in order for this to be so, their input signals must become zero. We have, therefore

From Eqs. (8.28) and (8.29)

Hence Eqs. (8.39) — (8.41) are simultaneously satisfied only for

and

Thus, under steady condition change in the tie line power and frequency of each area is zero. This has been achieved by integration of ACEs in the feedback loops of each area.

Dynamic response is difficult to obtain by the transfer function approach (as used in the single area case) because of the complexity of blocks and multi-input (ΔP_D1, ΔP_D2)  and multi-output (ΔP_tie,1, ΔP_tie,2, Δf₁, Δf₂) situation. A more organized and more conveniently carried out analysis is through the state space approach (a time domain approach). Formulation of the state space model for the two-area system.

The results of the two-area system (ΔP_tie, change in tie line power and Δf, change in frequency) obtained through digital computer study are shown in the form of a dotted line. The Two Area Load Frequency Control are assumed to be identical with system parameters given by