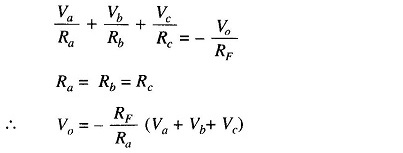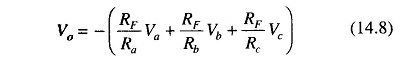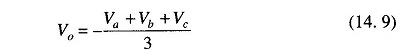Summing Amplifier Circuit Diagram:

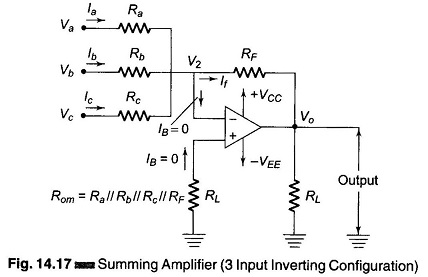
Figure 14.17 shows an Summing Amplifier circuit diagram in inverting configuration with three inputs V_a, V_b, V_c. Depending on the relation between R_a, R_b, R_c and R_F, the circuit can be used as a Summing amplifier, Scaling amplifier or Average amplifier.

Using Kirchoff‘s circuit equation, we have l_a + l_b + l_c = I_B + I_f. But I_B ≡ 0 and V₁ ≡ V₂ ≡ 0

Therefore

i.e.

In this circuit R_a = R_b = R_c = R_F.

Therefore

Hence the output voltage is the negative sum of all the input voltages. If each input voltages is amplified by a different factor, i.e. weighted differently at the output, the circuit is called a scaling or weighted amplifier (Fig. 14.17). The condition can be obtained by making R_a, R_b, and R_c, different in value. The output voltage of the scaling amplifier is then

where R_F/R_a ≠ R_F/R_b ≠ R_F/R_c.

Figure 14.17 can be modified to be used as an average amplifier. In this amplifier, the output voltage is the average value of the input voltages. This modification can be obtained by making R_a = R_b = R_c = R. Also, the gain by which input is amplified must be equal to 1 over the number of inputs, i.e. R_F/R = 1/n where n is the number of inputs. Therefore the output voltage is given by V_o = V_a + V_b + V_c.

Therefore the output voltage for three inputs is R_F/R = 1/3. The output voltage is given by