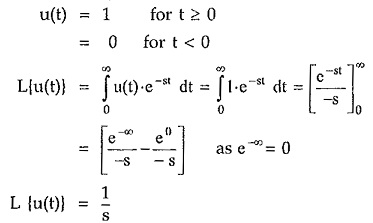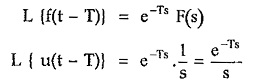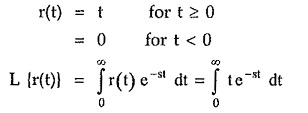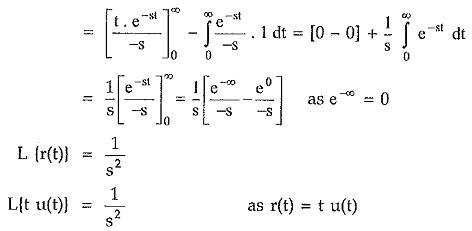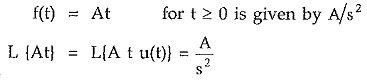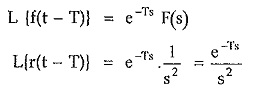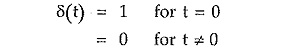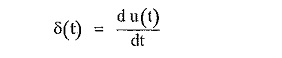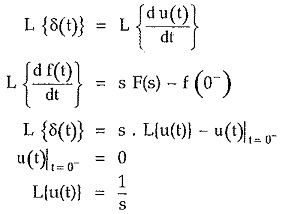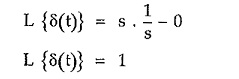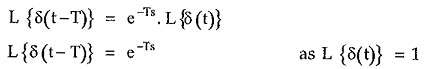Laplace Transform of Standard Functions:
The Laplace Transform of Standard Functions is given by
Step Function:
The unit step function is,
If there is step of amplitude A i.e. f(t) = A u(t) then its Laplace is given by A/s.
If the unit step is delayed by T instants then,
From the shifting theorem of Laplace transform we can write,
Ramp Function:
The unit ramp function is defined as,
Integrating by parts,
While the Laplace transform of ramp having slope A i.e.
If the unit ramp is shifted by T instants then,
From the shifting theorem of Laplace transform,
Impulse Function:
The unit impulse function is δ(t) and defined as,
We know the relation between unit step and unit impulse.
Taking Laplace transform of both sides,
If there is a delayed impulse function δ(t – T) then using shifting property we can write,
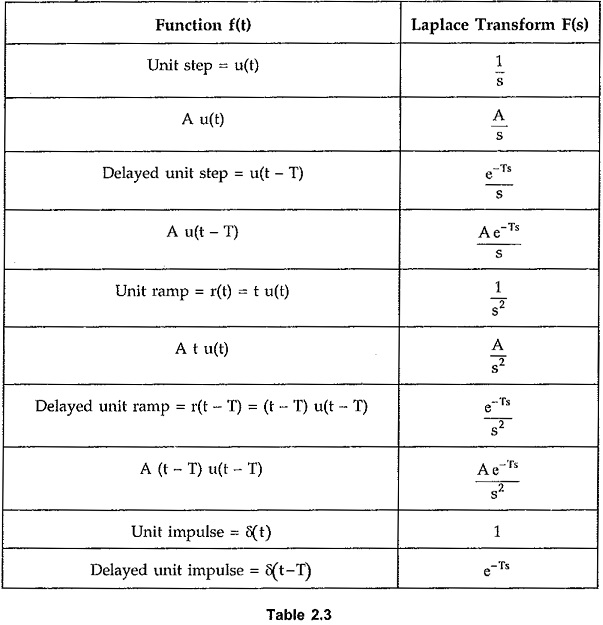
Let us summarise these results in the tabular form so that while finding the Laplace transform of the various time functions this table of standard Laplace transforms can be referred directly.
Thus the Laplace transforms of standard time functions are very useful to obtain the Laplace transform of any waveform by resolving it into standard function.