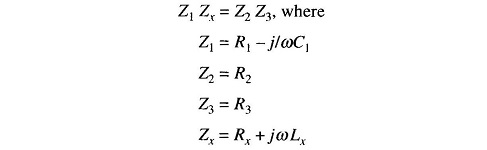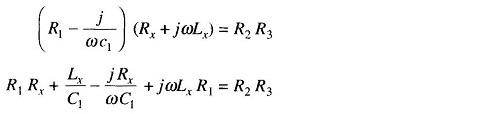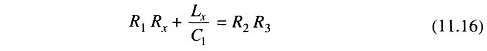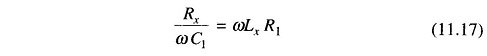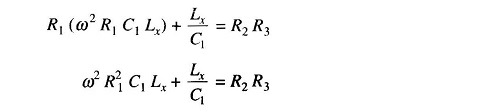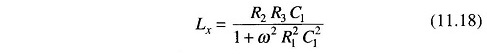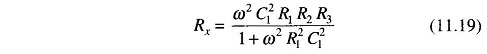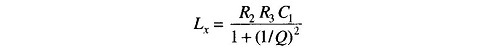Hays Bridge Circuit:

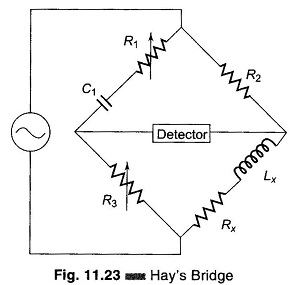
Hays Bridge Circuit, shown in Fig. 11.23, differs from Maxwell’s bridge by having a resistance R₁ in series with a standard capacitor C₁ instead of a parallel. For large phase angles, R₁ needs to be low; therefore, this bridge is more convenient for measuring high-Q coils. For Q = 10, the error is ± 1%, and for Q = 30, the error is ± 0.1%. Hence Hay’s bridge is preferred for coils with a high Q, and Maxwell’s bridge for coils with a low Q.

At balance

Substituting these values in the balance equation we get

Equating the real and imaginary terms we have

and

Solving for L_x and R_x we have, R_x = ω²L_xC₁R₁.

Substituting for R_x in Eq. (11.16)

Multiplying both sides by C₁ we get

Therefore,

Substituting for L_x in Eq. (11.17)

The term ω appears in the expres­sion for both L_x and R_x. This indicates that the bridge is frequency sensitive.

The Hays Bridge Circuit is also used in the measurement of incremental induct­ance. The inductance balance equation depends on the losses of the inductor (or Q) and also on the operating fre­quency.

An inconvenient feature of this bridge is that the equation giving the balance condition for inductance, contains the multiplier 1/(1 + 1/Q²). The inductance balance thus depends on its Q and frequency.

Therefore,

For a value of Q greater than 10, the term 1/Q² will be smaller than 1/100 and can be therefore neglected.

Therefore L_x = R₂R₃C₁, which is the same as Maxwell’s equation. But for inductors with a Q less than 10, the 1/Q² term cannot be neglected. Hence this bridge is not suited for measurements of coils having Q less than 10. A commercial bridge measure from 1 μ H – 100 H with ± 2% error.