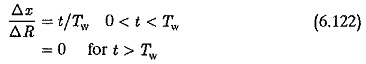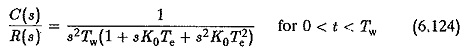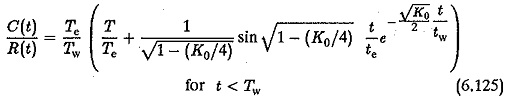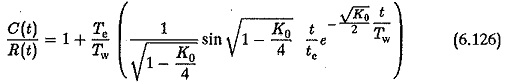Design of Controllers for Linearly Varying Inputs:
The Design of Controllers for Linearly Varying Inputs discussed in the foregoing sections are for the step input. The performance has been found to depend very much upon the value of integration time in relation to the uncompensated time constant of the plant. A control system is normally employed in situations where the controlled quantity (output) has to follow its reference value (input). If the changes in the input are very fast a controller having a small value of Ke (and hence small value of T0) is prohibited, as this results in a lightly damped system with a large overshoot.
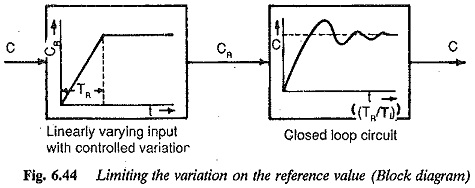
The oscillatory behaviour does not provide the necessary requirement if the input changes very fast. Also in some drive applications, the input is not a fast changing quantity. The dynamic behaviour of the load influences the operation of the controller. The dynamic performance of load is, however, taken to be very fast. From the above considerations, the rate of change of the input is limited for the system having a poor damping, i.e., very steep variation of the input is prohibited. A constant variation of the input to the controllers is achieved by means of limiters. A limiter is provided before the controller to see that the input to the controller does not change very fast but provides a suitable rate of change. The block diagram of such an arrangement is shown in Fig. 6.44. The transfer relation of the limiter is
The transfer function is
The transfer function of the total system is
Using the convolution integral the output of the system is
The damped periodic transient term of the response depends upon Te/Tw. From the expression it can be seen that the transient term is absent if the input value changes very slowly. In this case the controlled quantity follows the input very closely. The oscillatory behaviour of the system is completely eliminated. The system can be designed for low damping if the input changes slowly. Thus, a lightly damped system can be made to have a linearly changing input to the controller. The Design of Controllers for Linearly Varying Inputs has a lower phase margin, is generally sensitive to errors and is always in stability limits.
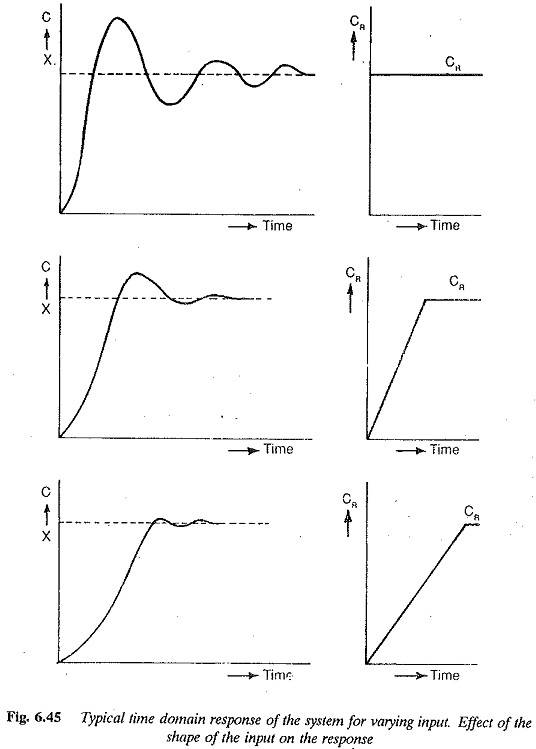
The time responses of a typical system for step as well as linearly varying inputs are shown in Fig. 6.45. The effect of variation of Tw (in relation to Te) is very clear from the figure. A proper choice of Tw controls or even eliminates the overshoot and the output is made to follow the input. If the variation of the input is slow the transient conditions in the system are the least.