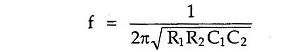Wien Bridge Oscillator using Op Amp:
This is also RC oscillator which uses RC type of feedback network. The main difference between phase shift and Wien bridge oscillator is that the R-C phase shift oscillator introduces 180° phase shift during the amplifier stage, while Wien bridge oscillator uses a non-inverting amplifier. So in Wien bridge type there is no phase shift necessary through the feedback network. Let us see the basic version of the Wien bridge oscillator and its analysis.
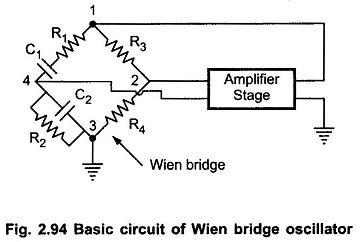
A basic Wien bridge and an amplifier stage is shown in the Fig. 2.94.
The output of the amplifier is applied between the terminals 1 and 3, which is the input to the feedback network. While the amplifier input is supplied from the diagonal terminals 2 and 4, which is the output from the feedback network. Thus amplifier supplies its own input through the Wien bridge as a feedback network.
The two arms of the bridge, namely R1,C1 in series and R2,C2 in parallel are called frequency sensitive arms. This is because the components of these two arms decide the frequency of the oscillator. Such a feedback network is called lead-lag network. This is because at very low frequencies it acts like a lead while at very high frequencies it acts like lag network
Wien Bridge Oscillator using Op amp:
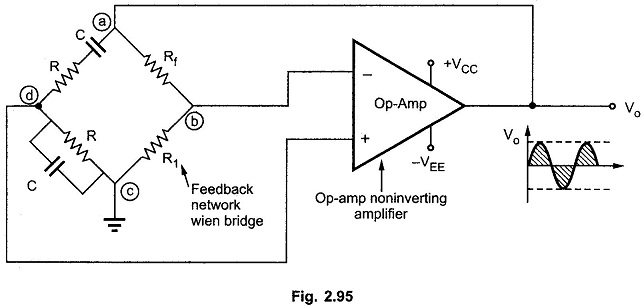
The Fig. 2.95 shows the Wien bridge oscillator using an op-amp.
The resistance R and capacitor C are the components of frequency sensitive arms of the bridge. The resistance Rf and R1 form the part of the feedback path. The gain of noninverting op-amp can be adjusted using the resistance Rf and R1. The gain of op-amp is,
To satisfy Barkhausen criterion that Aβ ≥ 1 it is necessary that the gain of the noninverting op-amp amplifier must be minimum 3.
Thus ratio of Rf and R1 must be greater than or equal to 2.
The frequency of oscillations is given by,
The feedback is given to the noninverting terminal of op-amp which ensures zero phase shift. It is used popularly in laboratory signal generators.
If in a Wien bridge feedback network, two resistances are not equal i.e. they are R1 and R2 while two capacitors are not equal i.e. they are C1 and C2 then the frequency of oscillations is given by,
With R1 = R2 = R and C1 = C2 = C we get it as 1/2πRC as stated earlier.
Advantages of Wien Bridge Oscillator:
The various advantages of Wien bridge oscillator are,
- By varying the two capacitor values simultaneously, by mounting them on the common shaft, different frequency ranges can be obtained.
- The perfect sine wave output is possible.
- It is useful audio frequency range i.e. 20 Hz to 100 kHz.
Disadvantages of Wien Bridge Oscillator:
If instead of op-amp, transistorised amplifier is to be- used then more stages are required to obtain 0° phase shift between input and output. This increases the number of components and cost. The frequency stability is poor.