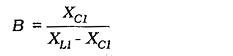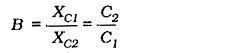Colpitts Oscillator using Op Amp:

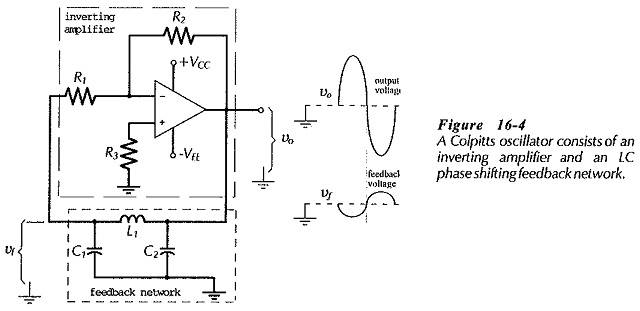
The Colpitts Oscillator using Op Amp circuit show in Fig. 16-4 is similar to the op-amp phase shift oscillator, except that an LC network is used to produce the necessary phase shift in the feedback voltage. In this case, the LC network acts as a filter that passes the oscillating frequency and blocks all other frequencies. The filter circuit resonates at the required oscillating frequency.

For resonance,

where X_CT is the total capacitance in parallel with the inductor. This gives the resonance frequency (and oscillating frequency) as,

Capacitors C₁ and C₂ are connected in series across L₁; so,

Consideration of the LC network shows that its attenuation (from the amplifier output to input) is due to the voltage divider effect of L and C_1. This gives,

It can be shown that the required 180° phase shift occurs when

and this gives,

As in the case of all oscillator circuits, the loop gain must be a minimum of one to ensure oscillation. Therefore,

or,

When deriving the above equations, it was assumed that the inductor coil resistance is very much smaller than the inductor impedance; that is, that the coil Q factor (ω L/R) is large. This must be taken into considered when selecting an inductor. It was also assumed that the amplifier input resistance is much greater than the impedance of C₁ at the oscillating frequency. Because of the inductor resistance and the amplifier input resistance, and because of stray capacitance effects when the oscillator operates at a high-frequency, the amplifier voltage gain usually has to be substantially larger than C₁/C₂.

Circuit Design:

Colpitts oscillator design can commence with selection of the smallest capacitor (C₂) much larger than stray capacitance, or with selection of a convenient value of L. To keep the amplifier input voltage to a fairly low level, the feedback network is often designed to attenuate the output voltage by a factor of 10. This requires that C₁/C₂ ≈ 10. (It should be recalled that large A_CL values require larger op-amp bandwidths.) Also, X_C2 should be much larger than the amplifier output impedance. Using the desired oscillating frequency, L can be calculated from Eq. 16-4. Amplifier input resistor R₁ must be large enough to avoid overloading the feedback network, (R₁ ≫ X_C1). Resistor R₂ is determined from A_CL and R₁.

BJT Colpitts Oscillator:

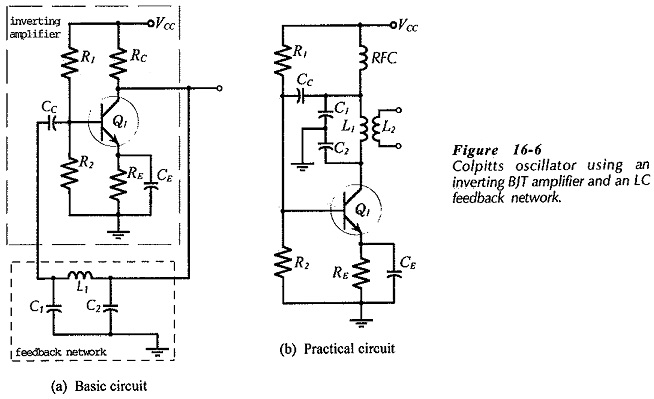
A Colpitts oscillator using a single BJT amplifier is shown in Fig. 16-6(a). This is the basic circuit, and its similarity to the op-amp Colpitts oscillator is fairly obvious. A more complex version of the circuit is shown in Fig. 16-6(b).

Components Q₁, R₁, R₂, R_E and C_E in (b) are unchanged from (a), but collector resistor R_C is replaced with inductor L₁. A radio frequency choke (RFC) is included in series with V_CC and L₁. This allows dc collector current (I_C) to pass, but offers a very high impedance at the oscillating frequency, so that the top of L₁ is ac isolated from V_CC and ground. The output of the LC network (L₁, C₁, C₂) is coupled to via C_c to the amplifier input. The circuit output voltage (v_o) is derived from a secondary winding (L₂) coupled to L₁. As in the case of the BJT phase shift oscillator, the transistor current gain is important. Circuit analysis gives Eq. 16-4 for frequency, and for current gain,