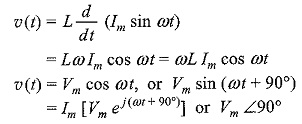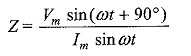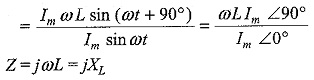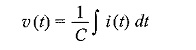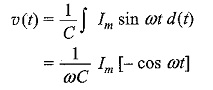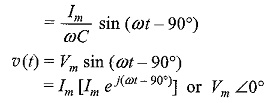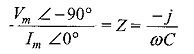Phase Relation in Pure Inductive Circuit:

Phase Relation in Pure Inductive Circuit – As discussed already, the voltage current relation in the case of an inductor is given by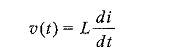

Consider the function i(t) = I_m sin ωt = I_m [ I_me^jωt ] or I_m∠0°

where

V_m = ωL I_m = X_LI_m

e^{j90° = j = 1 ∠90°}

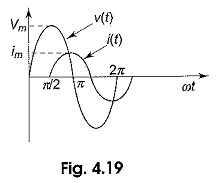
If we draw the waveforms for both, voltage and current, as shown in Fig. 4.19, we can observe the phase difference between these two waveforms.

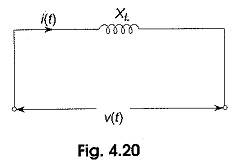
As a result, in a pure inductor the voltage and current are out of phase. The current lags behind the voltage by 90° in a pure inductor as shown in Fig. 4.20.

The impedance which is the ratio of exponential voltage to the corresponding current, is given by

where

V_m = ωL I_m

where X_L = ωL and is called the inductive reactance.

Hence, a pure inductor has an impedance whose value is ωL.

Phase Relation in Pure Capacitor:

As discussed already, the relation between voltage and current is given by

Consider the function i(t) = I_m sin ωt = I_m [ I_me^jωt ] or I_m∠0°

where

V_m = I_m/ωC

Hence, the impedance is Z = -j/ωC = -jX_C

Where X_C = 1/ωC and is called the capacitive reactance.

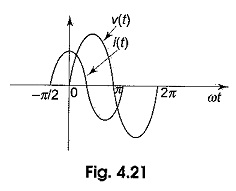
If we draw the waveform for both, voltage and current, as shown in Fig. 4.21, there is a phase difference between these two waveforms..

As a result, in a pure capacitor, the current leads the voltage by 90°. The impedance value of a pure capacitor