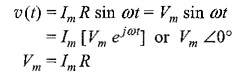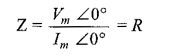Phase Relation in Pure Resistor:

Phase Relation in Pure Resistor – When a sinusoidal voltage of certain magnitude is applied to a resistor, a certain amount of sine wave current passes through it. We know the relation between υ(t) and i(t) in the case of a resistor. The voltage/current relation in case of a resistor is linear,

Consider the function

If we substitute this in the above equation, we have

where

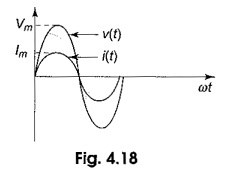
If we draw the waveform for both voltage and current as shown in Fig. 4.18, there is no phase difference between these two waveforms. The amplitudes of the waveform may differ according to the value of resistance.

As a result, in Phase Relation in Pure Resistor circuits, the voltages and currents are said to be in phase. Here the term impedance is defined as the ratio of voltage to current function.

With ac voltage applied to elements, the ratio of exponential voltage to the corresponding current (impedance) consists of magnitude and phase angles. Since the phase difference is zero in case of a resistor, the phase angle is zero. The impedance in case of resistor consists only of magnitude, i.e.