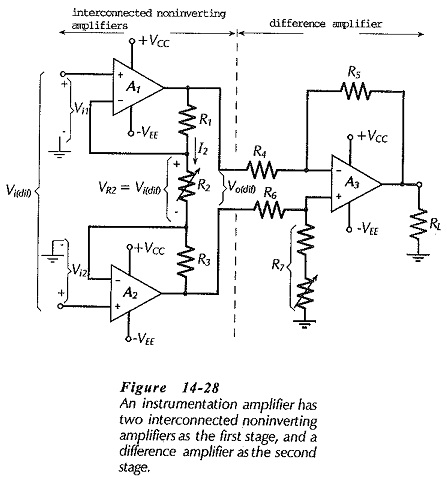
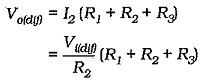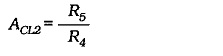Instrumentation Amplifier Circuit Working:

Circuit Operation – At first glance, the Instrumentation Amplifier Circuit Working in Fig. 14-28 looks complex, but when considered section by section it is found to be quite simple. First, note that the second stage (consisting of op-amp A₃ and resistors R₄ through R₇) is a difference amplifier. Next, look at A₁ and resistors R₁ and R₂; this is a noninverting amplifier. Similarly, A₂ combined with resistors R₂ and R₃ constitutes another noninverting amplifier. Because the first stage circuits share a single resistor, their operation is slightly different from the usual noninverting amplifier operation.

The first stage accepts a differential input voltage (V_i(dif)), and produces a differential output voltage (V_o(dif)). The differential input could be the difference between two grounded inputs (V_i1 and V_i2), as illustrated. But, is often a differential ungrounded input voltage derived, for example, from two voltage monitoring electrodes connected to a human body for medical purposes. In this case, there is often a large common mode input voltage, which can be shown to pass to the output of the first stage without amplification.

The difference amplifier second stage accepts V_o(dif) from the first stage as an input, and produces an output to a grounded load, as shown on the circuit diagram. As explained already, the difference amplifier tends to reject common-mode voltages, and the circuit can also have an adjustment for reducing common-mode outputs to zero.

The Instrumentation Amplifier Circuit Working is now seen to be a circuit with two high-impedance input terminals, and one low-impedance output. The differential input voltage is amplified and converted to a single-ended output, and common-mode inputs are attenuated.

Voltage Gain:

Recall that, with a noninverting amplifier, the feedback voltage to the op-amp inverting input terminal always equals the input voltage to the noninverting input terminal. Therefore, the voltage at the R₁R₂ junction equals V_i1, and that at the R₂R₃ junction equals V_i2. Consequently, the voltage drop across R₃ equals the difference between the two input voltages, which also means that V_R2 equals the differential input voltage (V_i(dif)). The current through R₂ can now be calculated as,

The voltage drop across R₁, R₂, and R₃ is the differential output voltage of the first stage (V_o(dif)).

The (closed-loop) voltage gain of the differential input-differential output first stage is,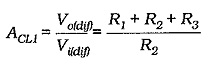

Normally, R₁ and R₃ are always equal. So, the first stage gain can be written as,

The second-stage gain is,

The overall voltage gain is,

The second stage is often designed for a gain of one, so that the overall voltage gain can be calculated from Eq. 14-19. Note that, as shown in Fig. 14-28, R₂ can be a variable resistor for adjustment of the circuit overall voltage gain.