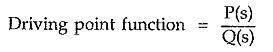Driving Point Function and Transfer Function:

For a given network, the ratio of Laplace transform of the source voltage and source current is called driving point function. If it is a ratio of source voltage to source current, it is called driving point impedance function denoted as Z(s) while if it is a ratio of source current to source voltage, it is called driving point admittance function denoted as Y(s).

The driving point impedance function is nothing but the input impedance of the network as viewed through the input terminals. As Y(s) is the reciprocal of Z(s), these functions are called immitance functions. While defining these functions, all initial conditions are assumed zero and there should not be any independent voltage or current sources present. The immitance function is always a ratio of two separate polynomials in ‘s’. Hence driving point function can be represented as,

Driving Point Function

where P(s) is numerator polynomial and Q(s) is denominator polynomial in s.

Necessary Conditions for Driving Point Functions:

After cancelling the common factors in the numerator polynomial P(s) and denominator polynomial Q(s), the necessary conditions for the driving point functions are as follows :

  • The coefficients of the numerator polynomial P(s) and the denominator polynomial Q(s) must be real and positive.
  • If poles and zeros are imaginary then such poles and zeros must be conjugate.
  • The real part of all the poles and zeros must be negative or zero and if the real part is zero, then the pole or zero must be simple.
  • There should not be any missing term between the highest and lowest degrees in the polynomials P(s) and Q(s) unless all the even or all the odd terms are missing.
  • The degree of the polynomial in numerator and denominator should differ by either zero or one.
  • The terms of lowest degree in P(s) and Q(s) may differ in degree at the most by one.

Transfer Functions:

The ratio of Laplace transform of a network parameter at one port to the Laplace transform of a network parameter at the other port and vice versa are called transfer functions. These functions may be voltage ratio functions or current ratio functions. Such functions may also represent transfer impedance or transfer admittance of the network. These are also determined under the same assumptions as all initial conditions are zero and no dependent current or voltage source is present in the network. The transfer functions are also the ratio of two separate polynomials in ‘s’.

Necessary Conditions for Transfer Functions:

After cancelling the common factors in the polynomials P(s) and Q(s), the necessary conditions for the transfer functions are as follows :

  • The coefficients of P(s) and Q(s) must be real and positive.
  • The complex and imaginary poles and zeros must be conjugate.
  • The real part of the poles must be negative or zero and if it is zero, the pole must be simple, including origin.
  • There should not be any missing term between the highest and lowest degree of Q(s), unless all the even or odd terms are missing.
  • The polynomial P(s) may have negative terms or even some missing terms between the highest and lowest degree.
  • The degree of polynomial P(s) may be as small as zero independent of the degree of the polynomial Q(s).

Related posts:

  1. Driving Point Immittance Function
  2. RC Driving Point Impedance function
  3. Conditions For Driving Point Function
  4. Driving Axle Code for Locomotives
  5. RL Driving Point Impedance
  6. Transfer Function or Network Function
  7. Gate Function in Network Function
  8. Transfer Function of Armature Controlled DC Motor
  9. Transfer Function of a Field Controlled DC Motor
  10. Controller Transfer Function
  11. Function Generation and Linearisation
  12. Multi Break Function of Circuit Breaker
  13. Laplace Transform of Unit Step Function
  14. Ramp Function
  15. Laplace Transform of Impulse Function
  16. Poles and Zeros of Network Function
  17. Frequency Domain Network Function
  18. Transfer Function of Two Port Network
  19. Poles and Zeros of Transfer Function
  20. Shifted Unit Step Function