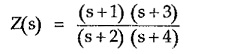RL Driving Point Impedance:

The RL networks consist of only R and L components. There is no capacitor present in such networks. The RL Driving Point Impedance of such networks is denoted as Z_RL(s). The properties of driving point impedance function of RL networks [Z_RL(s)] and the driving point admittance function of RC networks [Y_RC (s)] are exactly identical.

The RL impedance function is dual of RC admittance function. There are no complex poles in RL network functions and poles and zeros are located in left half of s-plane.

Consider the RL Driving Point Impedance network as,

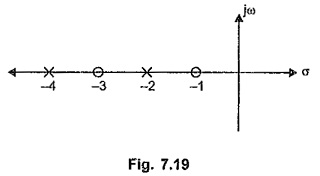
The poles are at s = – 2 and – 4 while the zeros are at s = – 1 and – 3.

The pole-zero plot is as shown in the Fig. 7.19.

Properties of RL Driving Point Impedance Functions:

Referring to the pole zero plot of Z_RL(s) function considered above, the various properties of RL, driving point impedance functions can be stated as,

1. The poles and zeros are simple. There are no multiple poles and zeros.
2. The poles and zeros are located on negative real axis.
3. The poles and zeros interlace each other on the negative real axis.
4. The poles and zeros are the critical frequencies. The critical frequency nearest to the origin is always a zero, which may be located at the origin.
5. The critical frequency at a greatest distance away from the origin is always a pole, which may be located at infinity also.
6. Partial fraction expansion of Z_RL(s) gives the residues which are negative and real hence to obtain positive residues the expansion of Z_RL(s)/s is obtained.
7. There can not be a pole at the origin.
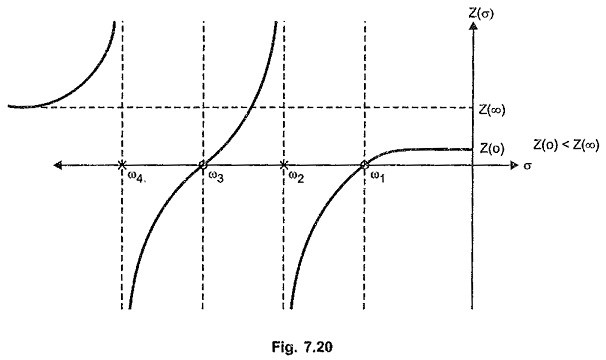
8. The slope of the graph of z (σ) against σ is always positive.
9. The value of Z_RL(s) at s = 0 is always less than the value of Z_RL(s)at s = ∞.

For the example considered Z_RL(0) = 3/8 while Z_RL(∞) = 1.

It can be easily verified from a simple RL network that the slope of the graph Z(σ) against σ is always positive.

The graph of Z(σ) against σ for the RL network function without a zero at the origin is shown in the Fig. 7.20.

ω₁,ω₂,ω₃ and ω₄ are the critical frequencies. At the critical frequencies like ω₂ and ω₄ the sign of Z(σ) changes suddenly such that the slope always remains positive.

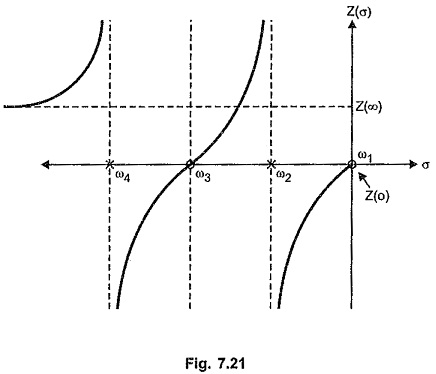
The nature of Z(σ) against σ graph for the RL network function when there is a zero at the origin is shown in the Fig. 7.21.

Realization of Impedance Function of RL Network:

The realization of Z_RL(s) function can be obtained using Foster I, Foster II, Cauer I and Cauer II forms. The number of elements are not equal to highest power of s in the overall Z(s) for RL networks.