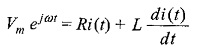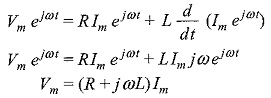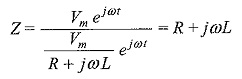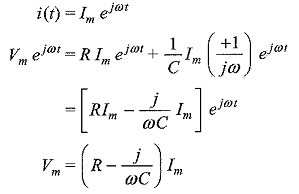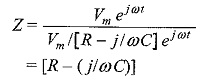Impedance Diagram:

Impedance Diagram is a complex quantity having real and imaginary parts; where the real part is the resistance and the imaginary part is the reactance of the circuit.

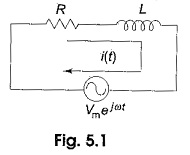
Consider the RL series circuit shown in Fig. 5.1. If we apply the real function  V_m cos ωt to the circuit, the response may be I_m cos ωt. Similarly, if we apply the imaginary function jV_m sin ωt to the same circuit, the response is jI_m sin ωt. If we apply a complex function, which is a combination of real and imaginary functions, we will get a complex response.

This complex function is V_m e^jωt = V_m(cos ωt + j sin  ωt).

Applying Kirchhoff s law to the circuit shown in Fig. 5.1,

we get

The solution of this differential equation is

By substituting i(t) in the above equation, we get

Impedance is defined as the ratio of the voltage to current function

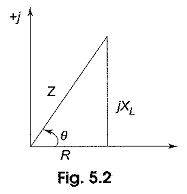
Complex impedance is the total opposition offered by the circuit elements to ac current, and can be displayed on the complex plane. The impedance is denoted by Z. Here the resistance R is the real part of the impedance, and the reactance X_L is the imaginary part of the impedance. The resistance R is located on the real axis. The inductive reactance X_L is located on the positive j axis. The resultant of R and X_L is called the complex impedance.

Figure 5.2 is called the impedance diagram for the RL circuit. From Fig. 5.2, the impedance Z = √R² +(ωL)², and angle θ = tan^–1 ωL/R. Here, the impedance is the vector sum of the resistance and inductive reactance. The angle between impedance and resistance is the phase angle between the current and voltage applied to the circuit.

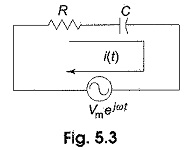
Similarly, if we consider the RC series circuit, and apply the complex function V_m e^jωt to the circuit in Fig. 5.3, we get a complex response as follows.

Applying Kirchhoff’s law to the above circuit, we get

Solving this equation we get,

The impedance

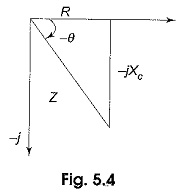
Here impedance Z consists of resistance (R), which is the real part, and capacitive reactance (X_C = 1/ωC), which is the imaginary part of the impedance. The resistance,R, is located on the real axis, and the capacitive reactance X_C is located on the negative j axis in the impedance diagram in Fig. 5.4.

Form Fig. 5.4, impedance Z = √R² + X²_C or √R² + (1+ωC)² and angle θ = tan^-1 (1/ωCR). Here, the impedance, Z, is the vector sum of resistance and capacitive reactance. The angle between resistance and impedance is the phase angle between the applied voltage and current in the circuit.