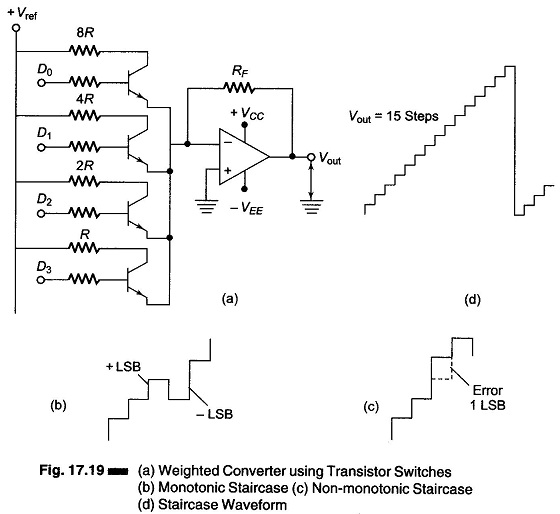
Weighted Converter Using Transistor Switches (Current Switch):
Figure 17.19 (a) shows a circuit diagram of a weighted converter, using transistor switches.
When the D bit is high (logic 1), it produces enough base current to saturate the transistor. When the D bit is low (logic 0), the base current is zero and the transistor remains off. Therefore, each transistor is in either saturation or cutoff, and acts as an open circuit or closed switch. If the D bits are the output of a counter, the output is 0000, 0001, …, 1111. The digital signal is converted into a continuous signal i.e. D/A conversion has taken place. One step is equal to an LSB increment. The resolution of the staircase is defined as the ratio of the LSB increment to the maximum output. Therefore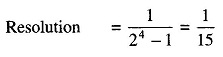
This is sometimes given as 1 part in 15 and
% Resolution = Resolution x 100
For a 4 bit converter, the % resolution is 1/15 x 100 = 6.67%.
The number of bits gives the resolution and an estimates number of steps. This converter is a weighted resistor converter. The accuracy of the output depends mainly on the tolerances of the weighted resistors. If they are exactly R, 2R, 4R and 8R, then all steps will be equal. If the resistances do not have these tolerances, the stairs (steps) will have non-equal steps. The various % resolutions for different numbers of bits are given in Table 17.6. The output staircase waveform is shown in Fig. 17.19(d).
When the weighted resistances used are of poor quality, the staircase produced will not be monotonic.
Monotonicity
A monotonic D/A converter is one that produce an increment in output for each increment in the input. The staircases voltages are nonmonotonic shown in Fig. 17.19 (c). For a monotonic converter the error permissible is less than + 1/2 LSB. Considering the worst case of + 1/2 LSB error, if it is followed by a — 1/2 LSB error, a critical level is produced, where the monotonicity is not lost as shown in Fig. 17.19 (b).
Disadvantage of Weighted Converter
The more the number of steps the converter has, the better the tolerances of the step, and the tolerances of resistance required. For example, if the staircase has 15 steps, the tolerance of the resistance should be less than + 6.67% (1/ 15). If the staircase has 255 steps, the resistance tolerances must be better than + 0.04% (1/255).
Therefore, for an 8 bit converter, resistance of a very high quality is required, which is a disadvantage. Another difficulty that arises with weighted resistors is that for an 8 bit we need resistances R, 2R, 4R, … 128 R. Therefore, the largest resistance is 128 times the smallest. For a 12 bit converter, the largest resistance must be 2048 times the smallest. Because of this disadvantage, it is not possible to produce mass weighted resistor D/A converters. Each converter has to be made and tested individually.