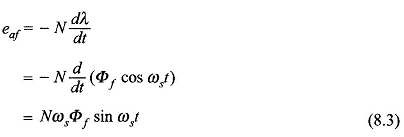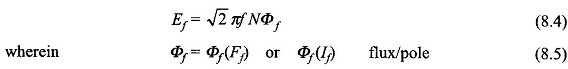Construction of Cylindrical Rotor Synchronous Machine:

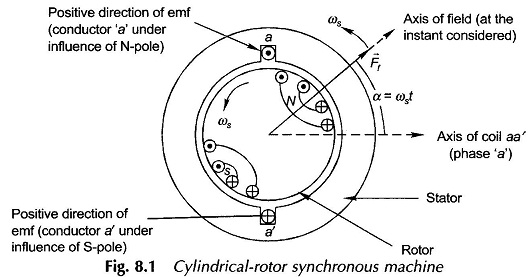
As stated earlier the Cylindrical Rotor Synchronous Machine offers constant permeance to mmf waves irrespective of the mechanical position of the rotor and is, therefore, simpler to model. Figure 8.1 shows the cross-sectional view of a 2-pole Cylindrical Rotor Synchronous Machine.

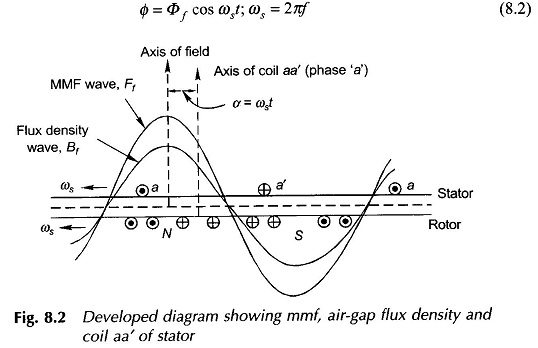
The rotor has distributed windings which produce an approximately sinusoidally distributed mmf wave in space rotating at synchronous speed ω_s rad (elect.)/s (n_s rpm) along with the rotor. This mmf wave is represented by the space vector F_f in the diagram and which at the instant shown makes an angle α = ω_st with the axis of coil aa’ on the stator (coil aa’ represents the phase a). The peak value of the vector F_f is F_f. As a consequence of the uniform air-gap, the mmf wave F_f produces sinusoidally distributed flux density wave B_f, in space phase with it. Figure 8.2 shows the developed diagram depicting the space phase relationship between B_f and E_f waves. As the rotor rotates (at synchronous speed ω_s), the B_f wave causes sinusoidally varying flux Φ to link with the coil aa’. The maximum value of this flux linkage is Φ_f, the flux per pole. Considering the time reference when F_f lies along the axis of coil aa’, this is a cosinusoidal variation, i.e.

It is, therefore, seen from Cylindrical Rotor Synchronous Machine that the flux linking the coil aa’ is a sinusoidal time variation and can be represented as the time phasor Φ_f. It will be referred to as flux phasor.

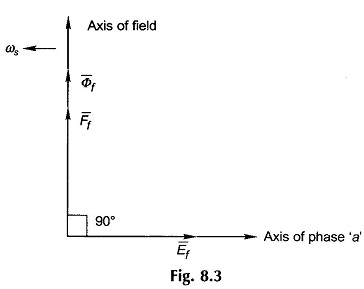
Consider now the space vector F_f as seen from the axis of coil aa’ on the stator. As F_f rotates at synchronous speed, it appears to be sinusoidally time-varying at ω_s = 2πf elect. rad/s as is evident from the developed diagram of Fig. 8.2. Furthermore, when the maximum positive value of F_f space wave is directed along the axis of coil aa’, the flux linkage of the coil has maximum positive value. It may, therefore, be considered that the rotating space vector F_f as seen from the stator is a time phasor F_f which is in phase with the flux phasor Φ_f as shown in Fig. 8.3. The magnitude relationship between Φ_f and F_f will be governed by the magnetization curve; this will be linear if the iron is assumed to be infinitely permeable in which case

where P = permeance per pole.

The emf induced in the coil aa’ of N turns is given by Faraday’s law,

The positive direction of the emf is indicated on the coil aa’. This is also verified by the flux cutting rule when conductor a lies under the influence of N-pole of the rotor and conductor a’ simultaneously lies under the influence of the S-pole. It immediately follows from Eqs (8.2) and (8.3) that the emf e_af represented as time phasor E_f lags behind the mmf phasor F_f and the flux phasor Φ_f by 90° as shown in Fig. 8.3. This figure also shows the relative location of the field axis and the axis of phase a wherein the axis of phase a is 90^° behind the rotor field axis. This is indicative of the fact that the field vector F_f lies 90° ahead of the axis of coil aa’ in Fig. 8.1 when the emf in coil aa’ has maximum positive value (projection of the phasor E_f on the axis of phase a). The rotor field axis is known as the direct-axis and the axis at 90° elect. from it is known as the quadrature-axis.

It immediately follows from Eq. (8.3) that the rms value of the emf induced in coil aa’ is

I_f being the direct current in the rotor field. Equation (8.5) between the flux/pole and field current is indeed the magnetization characteristic. Equation (8.4) suitably modified for a distributed (and also possibly short-pitched) stator winding is

It easily follows that the emfs produced in the other phases of the stator would progressively differ in time phase by 120°.

The conclusions drawn from the above discussion are indeed general and are reproduced below.

Whenever the magnetic structure of a Cylindrical Rotor Synchronous Machine is subjected to rotating mmf vector, it is seen as an mmf phasor from the stator with its flux phasor in phase with it, while the phasor representing the phase emf induced lags behind both these phasors by 90° (see Fig. 8.3).

It was shown in already that when a 3-phase stator supplies a balanced load, it sets up its own mmf vector F_ar (sinusoidally distributed in space), called the armature reaction, rotating at synchronous speed in the same direction as the rotor. The magnetic circuit is now subjected to two rotating mmf vectors F_f and F_ar, both rotating at synchronous speed with a certain angle between them. The objective here is to establish what determines this angle.

To begin with, it is observed from Cylindrical Rotor Synchronous Machine that in the generating operation of the machine, the emf and current have the same positive direction. Consider the case when the current I_a supplied by the coil aa’ is in phase with the coil emf E_f. It means that at the time instant when the emf is maximum positive in the coil aa’, its current also has maximum positive value. The emf in coil aa’ will be maximum positive when the field mmf vector F_f is 90° ahead of the coil axis (in the direction of rotation) as shown in Fig. 8.4(a). Simultaneously, F_ar is directed along the axis of coil aa’ which has maximum positive current at this instant. It is therefore, seen from Fig. 8.4(a) that F_f is 90° ahead of F_ar when E_f and I_a are in phase. The resultant mmf vector F_r is the vector sum

as shown in Fig. 8.4(a). It is observed that F_r lags F_f by angle δ. The corresponding phasor diagram, drawn as per the general conclusions stated earlier, is shown in Fig. 8.4 (b) wherein the phasor equation corresponding to the vector Eq. (8.7) is

It is observed from the phasor diagram that l_a and F_ar are in phase; this is logical because F_ar is produced by l_a and is proportional to it. The resultant mmf vector F_r produces the resultant air-gap flux phasor Φ_r which in turn induces the emf E_r in phase a lagging 90° behind the phasor F_r. The phase emf E_r induced in the machine, called air-gap emf, lags by angle δ behind E_f (emf induced by F_f acting alone) which is the same angle by which F_r lags behind E_f in the vector diagram of Fig. 8.4(a) or the angle by which F_r lags behind F_f in the phasor diagram of Fig. 8.4(b). E_f is known as the excitation emf.

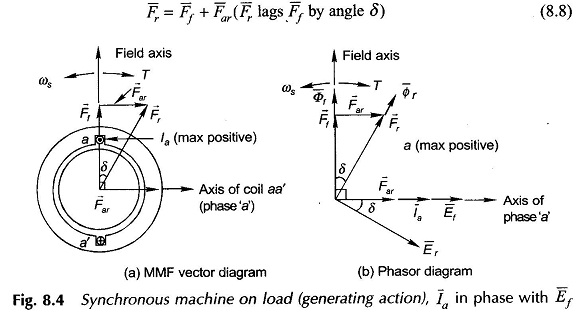
In case l_a lags E_f by an angle ψ, the positive current maximum in the coil aa’ will occur angle ψ later, so that F_f now lies (90° + ψ) ahead of F_ar as shown in the vector diagram of Fig. 8.5(a). The corresponding phasor diagram is shown in Fig. 8.5(b) wherein F_f leads F_ar by (90° + ψ). The phase angle between E_r and I_a indicated by θ is the power factor angle provided it is assumed that the armature has zero resistance and leakage reactance so that the machine terminal voltage

It is seen from Figs 8.5(a) and (b) that the field poles lie an angle δ ahead of the resultant mmf (or resultant flux) wave. The electromagnetic torque developed in the machine tries to align the field poles with the resultant field and is, therefore, in a direction as shown in Fig. 8.5(a) as well as in Fig. 8.5(b). It is immediately seen that the torque on the field poles is in opposite direction to that of rotation which means that mechanical power is absorbed by the machine. This is consistent with the assumed condition of the generating action (positive current in the direction of positive emf). It may, therefore, be concluded that in generating action, the field poles are driven ahead of the resultant flux wave by an angle δas a consequence of the forward acting torque of the prime mover. Also, the field poles are dragged behind by the resultant flux from which results the conversion of mechanical energy into electrical form.

As already shown, if the magnetic circuit is assumed linear, the magnitude of the torque is given by

where Φ_r is the resultant flux/pole, F_f the peak value of field ampere-turns and δ is the angle by which F_f leads F_r. It is also observed from Fig. 8.5(b) that E_f also leads E_r by the same angle δ.

When F_f and Φ_r are held constant in magnitude, the machine meets the changing requirements of load torque by adjustment of the angle δ which is known as the torque (power) angle.

The torque expression of Eq. (8.9) can also be written in terms of voltages as

where

• E_r = emf induced in the machine under loaded condition; called air-gap emf.
• E_f = emf induced by the field mmf F_f acting alone, i.e. the machine is on no-load with same F_f (or rotor field current) as on-load; called excitation emf.

The value of the constant K will be found in Sec. 8.8.

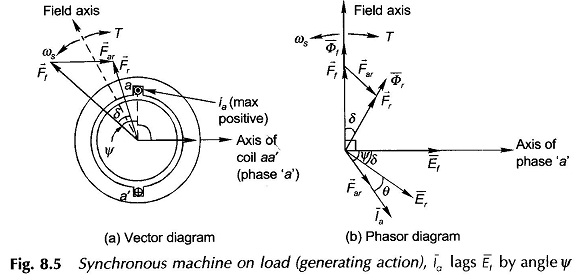
In motoring action of the Cylindrical Rotor Synchronous Machine, the positive current flows opposite to the induced emf. Since the phasor diagrams above have been drawn with the convention of generating current (i.e. current in the direction of emf), the armature reaction phasor F_ar will now be located by phase reversing the motoring current for consistency of convention. Accordingly the phasor diagram for motoring action is drawn in Fig. 8.6. It is immediately observed from this figure that F_f and E_f now lag F_r and E_r respectively by angle δ. The torque of electromagnetic origin therefore acts on the field poles in the direction of rotation so that the mechanical power is output meaning thereby motoring action.

If the terminal voltage V_t = E_r and its frequency is held constant by an external 3-phase source, called infinite bus, the machine operates as a generator (Fig. 8.5) or as a motor (Fig. 8.6) depending upon the mechanical conditions at a shaft.

Figure 8.3 is representative of no-load conditions when the machine is said to be floating on busbars with zero stator current and the rotor being run at synchronous speed by external means (prime mover). If mechanical power from the prime mover is now increased, the field poles (rotor) move ahead causing current to be fed into the bus-bars. Under steady condition, the field poles lie ahead of the resultant flux wave by angle δ (Figs. 8.4 and 8.5) creating electromagnetic torque in opposition to the direction of rotor rotation; the value of δcorresponds to the balance of torques (or power, P = Tω_s). The electrical power output is

which balances the mechanical power input from the primemover because there are no losses in the stator (resistance is assumed to be zero). Here I_a is the generating current taken to be positive in the direction of the machine’s induced emf E_r.

If instead, the shaft is mechanically loaded from the no-load condition (Fig. 8.3), the field poles lag behind the resultant flux wave as in Fig. 8.6 creating electromagnetic torque in the direction of rotation thereby outputting mechanical power; the electrical input power being 3V_t(= E_r)I_a cos θ, where I_a is the motoring current taken as positive in opposition to the positive direction of E_r.

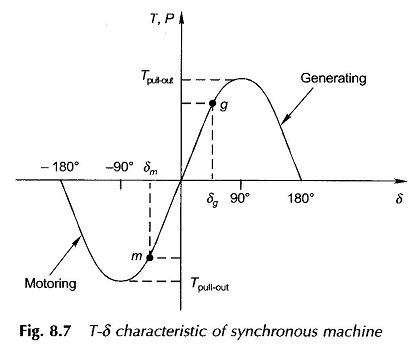
The torque (power)-angle (T-δ) relationship of Eq. (8.10) for fixed E_f and E_r(=V_t) is drawn in Fig. 8.7 with δ taken as positive for generating action and negative for motoring action. The operating points as the generator and motor are indicated by g and m on this curve corresponding to the specific condition of loading. The characteristic exhibits, both in generating and motoring operation, a maximum torque at δ = 90°, called the pull-out torque, beyond which the Synchronous link between field poles and the resultant flux wave is severed and the machine falls out-of-step (or loses synchronism). The average developed machine torque now becomes zero and so the average electric power fed by the generating machine to the bus-bars, (infinite) or average electric power drawn by the motoring machine from the bus bars reduces to zero. The generating machine thus accelerates and so overspeeds (primemover power is assumed to remain constant) and the motoring machine decelerates and comes to stop.