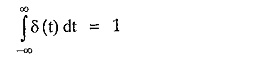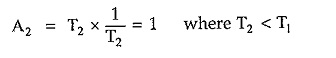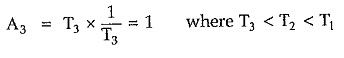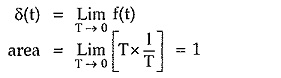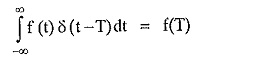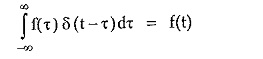Laplace Transform of Impulse Function:
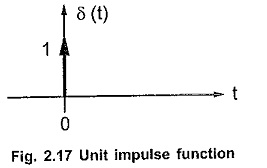
The Laplace Transform of Impulse Function is a function which exists only at t = 0 and is zero, elsewhere. The impulse function is also called delta function. The unit impulse function is denoted as δ(t). The amplitude of impulse function is infinitely large at t = 0, but for unit impulse function the area under the curve is equal to one. The unit impulse function is shown in the Fig. 2.17.
The one, in the Fig. 2.17 near arrow, indicates the area under the pulse.
Mathematically it is represented as, δ(t) = 0 t ≠ 0
and area under the pulse is unity i.e.
The concept of unit impulse function can be further simplified by the following discussion.
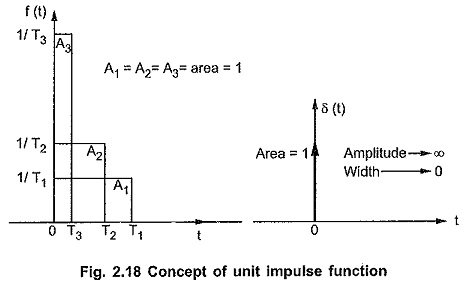
Consider a rectangular pulse of unit area having width T1 and amplitude 1/T1.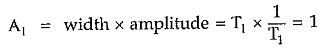
If now width is decreased from T1 to T2 then to have unit area of pulse its amplitude must increase from 1/T1 to 1/T2
If the width is further decreased to T3 then to have unit area of pulse its amplitude will further increase to 1/T3.
In the limiting case now if the width tends to zero then the amplitude of the pulse tends to infinity to get the unit area. Such a function i.e. pulse with infinite amplitude and zero width, having unit area under the pulse is called unit impulse function or delta function.
From the Fig. 2.18 we can write that if f(t) is the pulse with width T then the unit impulse function is,
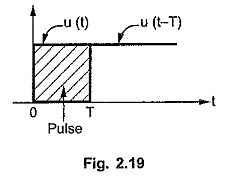
The unit impulse function can also be obtained using step functions. The unit impulse function is the limiting case of a rectangular pulse. A rectangular pulse can be obtained by subtraction of two step functions as shown in the Fig. 2.19.
Hence the rectangular pulse can be expressed as,
this is a pulse of width T.
Hence unit impulse function having unit area under pulse can be written as,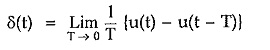
Delayed Unit Impulse Function:
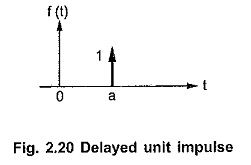
Similar to the delayed step and ramp, there can exist a delayed unit impulse function.
It has an unit area, but existing at t = a as shown in the Fig. 2.20. It is denoted as,
Important Properties of Impulse Function:
There are two important properties of impulse functions.
Shifting Property :
Mathematically this property is expressed by the integral,
where δ(t — T) is delayed impulse function.
Replication Property :
This property is mathematically given by,
This property tells that the convolution of any function with an impulse function results into the original function.