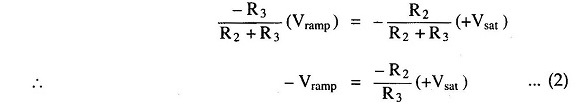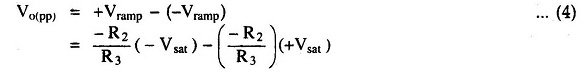Triangular Wave Generator Using Op amp:

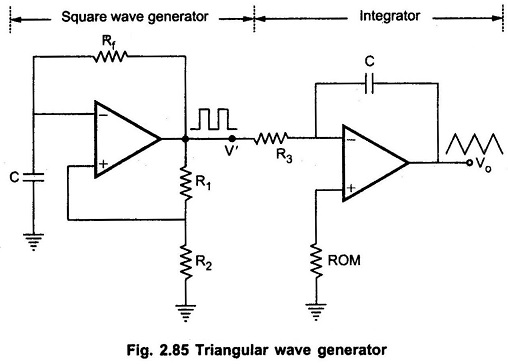
We have seen that, the output of integrator is a Triangular Wave Generator Using Op amp if its input is a square wave. This means that a Triangular Wave Generator Using Op amp can be formed by simply connecting an integrator to the square wave generator as shown in the Fig. 2.85.

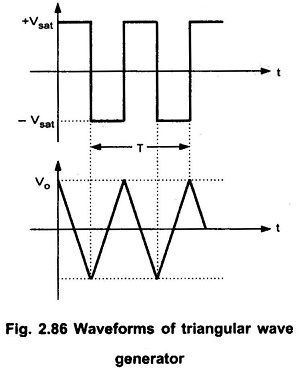
Basically, triangular wave is generated by alternatively charging and discharging a capacitor with a constant current. This is achieved by connecting integrator circuit at the output of square wave generator. Assume that V’ is high at +V_sat. This forces a constant current (+V_sat/R₃) through C (left to right) to drive V_o negative linearly. When V’ is low at -V_sat, it forces a constant current (-V_sat/R₃) through C (right to left) to drive V_o positive, linearly. The frequency of the triangular wave is same as that of square wave. This is illustrated in Fig. 2.86. Although the amplitude of the square wave is constant (± V_sat), the amplitude of the triangular wave decreases with an increase in its frequency, and vice versa. This is because the reactance of capacitor decreases at high frequencies and increases at low frequencies.

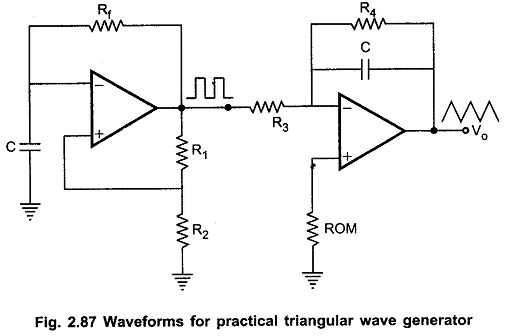
In practical circuits, resistance R₄ is connected across C to avoid the saturation problem at low frequencies as in the case of practical integrator as shown in the Fig. 2.87.

To obtain stable triangular wave at the output, it is necessary to have 5R₃ C₂ > T/2, where T is the period of the square wave input.

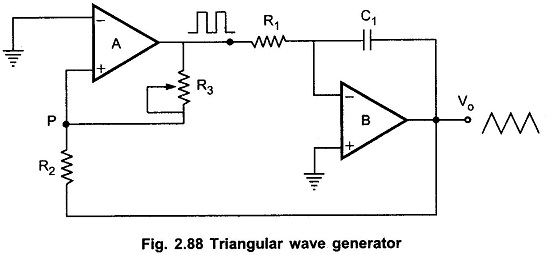
Another triangular wave generator, which requires fewer components, is shown in the Fig. 2.88.

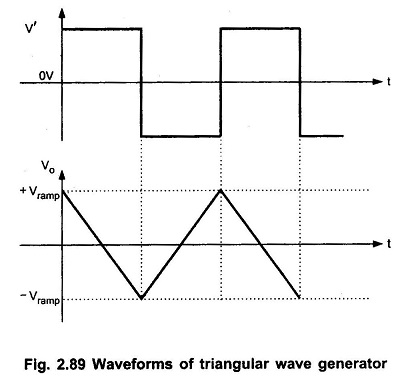
It consists of a comparator (A) and an integrator (B). The output of comparator A is a square wave of amplitude ± V_sat and is applied to the inverting (-) input terminal of the integrator B. The output of integrator is a triangular wave and it is feedback as input to the comparator A through a voltage divider R₂ R₃.

To understand circuit operation, assume that the output of comparator A is at + V_sat . This forces a constant current (+ V_sat/R₁) through C to give a negative going ramp at the output of the integrator, as shown in the Fig. 2.88. Therefore, one end of voltage divider is at a voltage +V_sat and the other at the negative going ramp. When the negative going ramp reaches a certain value -V_ramp, the effective voltage at point p becomes slightly below 0V.

As a result, the output of comparator A switches from positive saturation to negative saturation (-V_sat). This forces a reverse constant current (right to left) through C to give a positive going ramp at the output of the integrator, as shown in the Fig. 2.89. When positive going ramp reaches + V_ramp, the effective voltage at point p becomes slightly above 0V. As a result, the output of comparator A switches from negative saturation to positive saturation (+V_sat). The sequence then repeats to give triangular wave at the output of integrator B.

Amplitude and Frequency Calculations:

The frequency and amplitude of the Triangular Wave Generator Using Op amp wave can be determined as follows :

When comparator output is at +V_sat, the effective voltage at point P is given by

When effective voltage at P becomes equal to zero, we can write above equation as,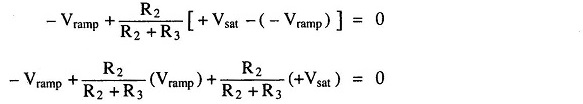

Similarly, when comparator output is at -V_{sat ,}we can write,

The peak to peak amplitude of the triangular wave can be given as

If | +V_sat| = |-V_sat| then, we can write

The time taken by the output to swing from – V_ramp to + V_ramp (or from + V_ramp to – V_ramp) is equal to half the time period T/2. Refer Fig. 2.89. This time can be calculated from the integrator output equation as follows :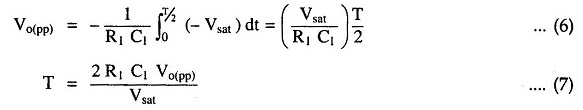

Substituting value of V_o(pp) we get,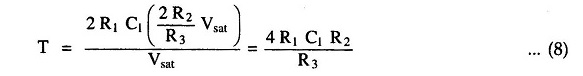

Therefore, the frequency of oscillation can be given as,