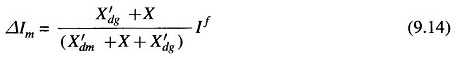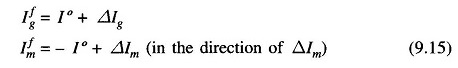Short Circuit Current Computation through Thevenin Theorem:
An alternate method of computing Short Circuit Current Computation is through the application of the Thevenin theorem. This Short Circuit Current Computation method is faster and easily adopted to systematic computation for large networks. While the method is perfectly general, it is illustrated here through a simple example.
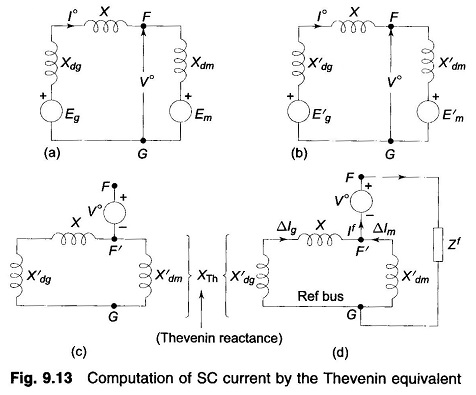
Consider a synchronous generator feeding a synchronous motor over a line. Figure 9.13a shows the circuit model of the system under conditions of steady load. Fault computations are to be made for a fault at F, at the motor terminals. As a first step the circuit model is replaced by the one shown in Fig. 9.13b, wherein the synchronous machines are represented by their transient reactances (or subtransient reactances if subtransient currents are of interest) in series with voltages behind transient reactances. This change does not disturb the prefault current I° and prefault voltage V° (at F).
As seen from FG the Thevenin equivalent circuit of Fig. 9.13b is drawn in Fig. 9.13c. It comprises prefault voltage V° in series with the passive Thevenin impedance network. It is noticed that the prefault current I° does not appear in the passive Thevenin impedance network. It is therefore to be remembered that this current must be accounted for by superposition after the SC solution is obtained through use of the Thevenin equivalent.
Consider now a fault at F through an impedance Zf . Figure 9.13d shows the Thevenin equivalent of the system feeding the fault impedance. We can immediately write
Current caused by fault in generator circuit
Current caused by fault in motor circuit
Postfault currents and voltages are obtained as follows by superposition:
Postfault voltage
where ΔV = -jXThIf is the voltage of the fault point F′ on the Thevenin passive network (with respect to the reference bus G) caused by the flow of fault current If.
An observation can be made here. Since the prefault current flowing out of fault point F is always zero, the postfault current out of F is independent of load for a given prefault voltage at F.
The above approach to SC computation is summarized in the following four steps:
- Step 1: Obtain steady state solution of loaded system (load flow study).
- Step 2: Replace reactances of synchronous machines by their subtransient/transient values. Short circuit all emf sources. The result is the passive Thevenin network.
- Step 3: Excite the passive network of Step 2 at the fault point by negative of prefault voltage (see Fig. 9.13d) in series with the fault impedance. Compute voltages and currents at all points of interest.
- Step 4: Postfault currents and voltages are obtained by adding results of Steps 1 and 3.
The following assumptions can be safely made in SC computations leading to considerable computational simplification:
- Assumption 1: All prefault voltage magnitudes are 1 pu.
- Assumption 2: All prefault currents are zero.
The first assumption is quite close to actual conditions as under normal operation all voltages (pu) are nearly unity.
The changes in current caused by Short Circuit Current Computation are quite large, of the order of 10-20 pu and are purely reactive; whereas the prefault load currents are almost purely real. Hence the total postfault current which is the result of the two currents can be taken in magnitude equal to the larger component (caused by the fault). This justifies assumption 2.