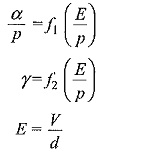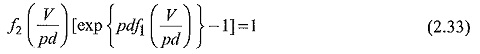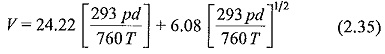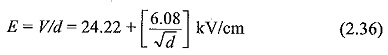Paschen Breakdown | Paschen’s Law | Paschen curve
It has been shown earlier (refer Sec. 2.6) that the Paschen Breakdown criterion in gases is given as
where the coefficients α and γ are functions of E/p, i.e
Substituting for E have in the expressions for α and γ and rewriting Eq. (2.26) we have
This equation shows a relationship between V and pd, and implies that the breakdown voltage varies as the product pd varies. Knowing the nature of functions f1 and f2 we can rewrite Eq. (2.32) as,
This equation is known as Paschen’s law.
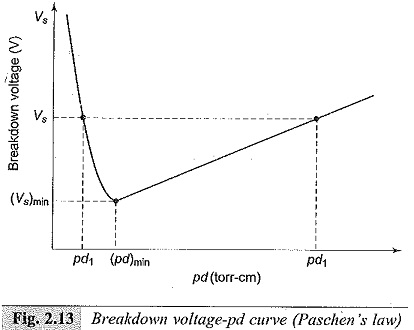
The Paschen’s curve, the relationship between V and pd is shown in Fig. 2.13. It is seen that the relationship between V and pd is not linear and has a minimum value for any gas.
This means that a breakdown voltage of a uniform field gap is a unique function of the product of p, the gas pressure and d, the electrode gap, for a particular gas and for a given electrode material.
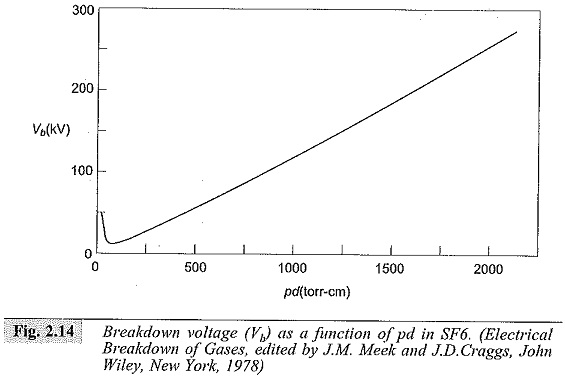
Paschen’s Law is found to be valid over a wide range of pd values as shown in Fig. 2.14. As can be seen from the figure, at higher pd values, the breakdown voltage in some gases is found to be slightly higher than the values at smaller gaps for the same values of pd. This departure from Paschen’s law is probably due to the transition from the Townsend breakdown mechanism to the Streamer mechanism. On the other hand, at very low pressures, deviations from the Paschen’s law are observed when the breakdown mechanism is not influenced by the properties of the gas but depends on the purity and property of the electrodes.
In order to account for the effect of temperature, the Paschen Breakdown is generally stated as V = f(Nd), where N is the density of the gas molecules. This is necessary, because the pressure of the gas changes with temperature according to the gas law pν = NRT, where ν is the volume of the gas, T is the temperature, and R is a constant.
Based on the experimental results, the breakdown potential of air is expressed as a power function in pd as
It may be noted from the above formula that the breakdown voltage at constant pressure and temperature is not constant.
At 760 torr and 293 K.
This equation yields a limiting value for E of 24 kV/cm for long gaps and a value of 30 kV/cm for (293 pd/760T) = 1, which means a pressure of 760 torr at 20°C with 1 cm gap. This is the usually quoted breakdown strength of air at room temperature and at atmospheric pressure.