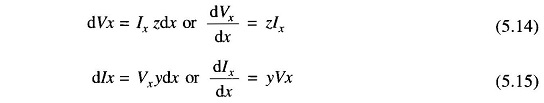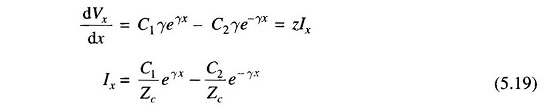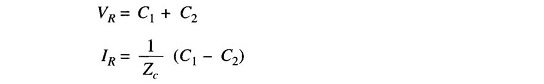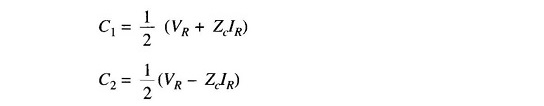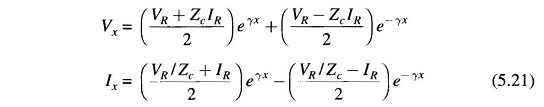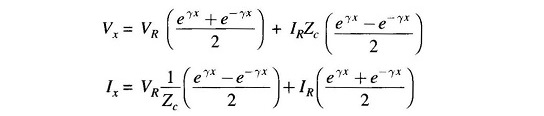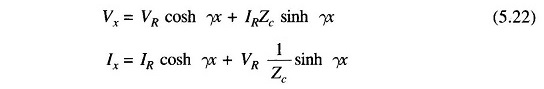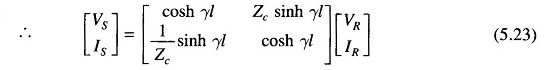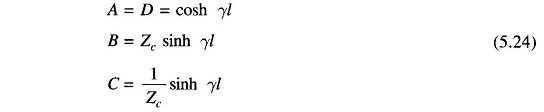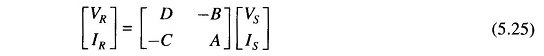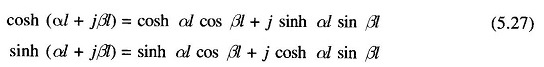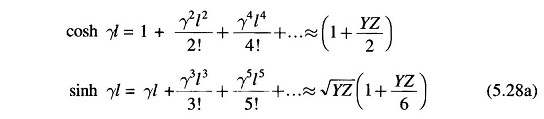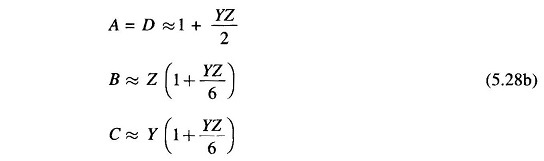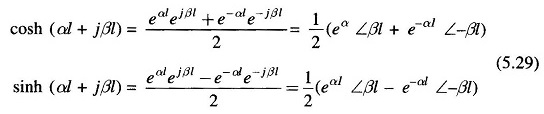Long Transmission Line:
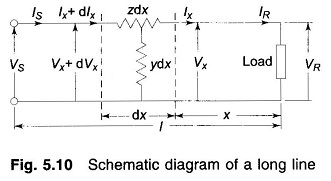
For lines over 250 km, the fact that the parameters of a line are not lumped but distributed uniformly throughout its length, must be considered. Figure 5.10 shows one phase and the neutral return (of zero impedance) of a Long Transmission Line.
Let dx be an elemental section of the line at a distance x from the receiving-end having a series impedance zdx and a shunt admittance ydx. The rise in voltage to neutral over the elemental section in the direction of increasing x is dVx. We can write the following differential relationships across the elemental section:
It may be noticed that the kind of connection (e.g. T or π) assumed for the elemental section, does not affect these first order differential relations. Differentiating Eq. (5.14) with respect to x, we obtain
Substituting the value of dIx/dx from Eq. (5.15), we get
This is a linear differential equation whose general solution can be written as follows:
where
and C1 and C2 are arbitrary constants to be evaluated.
Differentiating Eq. (5.17) with respect to x:
Where
The constants C1 and C2 may be evaluated by using the end conditions, i.e. when x = 0, Vx = VR and Ix = IR. Substituting these values in Eqs. (5.17) and (5.19) gives
which upon solving yield
With C1 and C2 as determined above, Eqs. (5.17) and (5.19) yield the solution for Vx and Ix as
Here Zc is called the characteristic impedance of the Long Transmission Line and γ is called the propagation constant.
Knowing VR, IR and the parameters of the line, using Eq. (5.21) complex number rms values of Vx and Ix at any distance x along the line can be easily found out.
A more convenient form of expression for voltage and current is obtained by introducing hyperbolic functions. Rearranging Eq. (5.21), we get
These can be rewritten after introducing hyperbolic functions, as
where x = l, Vx = Vs, Ix = Is
Here
In case [VS IS] is known, [VR IR] can be easily found by inverting Eq. (5.23).
Thus
Evaluation of ABCD Constants:
The ABCD constants of a long Long Transmission Line can be evaluated from the results given in Eq. (5.24). It must be noted that γ=√yz is in general a complex number and can be expressed as
The hyperbolic function of complex numbers involved in evaluating ABCD constants can be computed by any one of the three methods given below.
Method 1:
Note that sinh, cosh, sin and cos of real numbers as in Eq. (5.27) can be looked up in standard tables.
Method 2:
This series converges rapidly for values of γl usually encountered for power lines and can be conveniently approximated as above. The corresponding expressions for ABCD constants are
The above approximation is computationally convenient and quite accurate for lines up to 400/500 km.
Method 3: