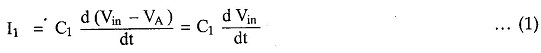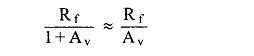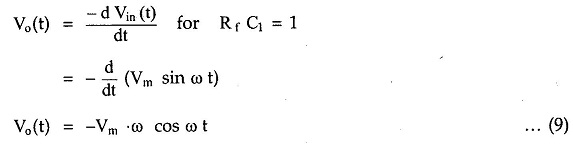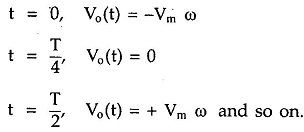Ideal Active Op Amp Differentiator circuit:
The circuit which produces the differentiation of the input voltage at its output is called Differentiator. The differentiator circuit which does not use any active device is called passive Differentiator. While the differentiator using an active device like op-amp is called an active Differentiator. Let us discuss the operation of Ideal Active Op Amp Differentiator circuit.
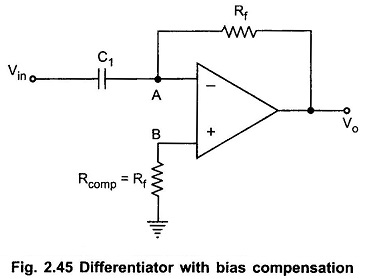
The Ideal Active Op Amp Differentiator circuit can be obtained by exchanging the positions of R and C in the basic active integrator circuit. The Op Amp Differentiator circuit is shown in the Fig. 2.44.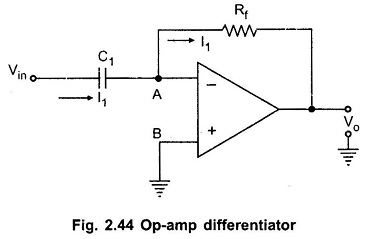
The node B is grounded. The node A is also at the ground potential hence VA = 0.
As input current of op amp is zero, entire current I1 flows through the resistance Rf.
From the input side we can write,
From the output side we can write,
Equating the two equations,
The equation shows that the output is C1Rf times the differentiation of the input and product C1Rf is called time constant of the differentiators.
The negative sign indicates that there is a phase shift of 180° between input and output. The main advantage of such an active differentiators is the small time constant required for differentiation.
By Miller’s theorem, the effective resistance between input node A and ground becomes
where
Av is the gain of the op-amp which is very large. Hence effective Rf becomes very very small and hence the condition RfC1 ≪ T gets satisfied at all the frequencies.
In practice a resistance Rcomp = Rf is connected to the noninverting terminal to provide the bias compensation. This is shown in the Fig. 2.45.
Input and Output Waveforms:
Let us study the output waveforms, for various input signals.
For simplicity of understanding, assume that the values of Rf and C1 are selected to have time constant (Rf C1) as unity.
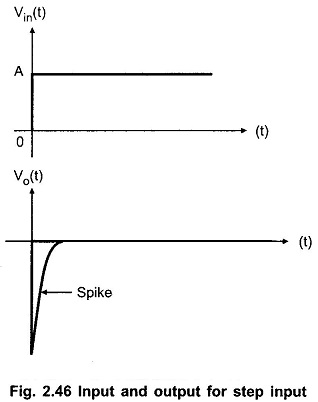
i) Step input signal:
Let the input waveform is of step type with a magnitude of A units. Mathematically it is expressed as,![]()
Now mathematically, the output of the differentiators must be,
This is because A is constant. Actually the step input takes a finite time to rise from 0 to A volts. Due to this finite time, the differentiator output is not zero but appears in the form of a spike at t = 0. As the circuit acts as an inverting differentiator, the negative going spike or pulse appears at t = 0 and after that output remains zero.
Both input and output waveforms of the differentiator with a step input, are shown in the Fig. 2.46.
ii) Square wave input signal:
The square wave is made of steps i.e. step of A volts from t = 0 to t = T/2, while a step of -A volts from t = T/2 to t = T and so on.
Mathematically it can be expressed as,
The differentiator behaves similar to its behavior to step input. For positive going pulse, the output shows negative going pulse and for negative going input, the output shows positive going pulse. Hence the total output for the square wave input is in the form of train of pulses or spikes.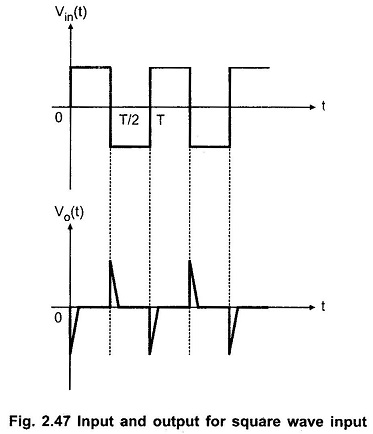
The input and output waveforms are shown in the Fig. 2.47.
iii) Sine wave input:
Let the input waveform be purely sinusoidal with a frequency of ω rad/sec. Mathematically it can be expressed as,
where Vm is the amplitude of the sine wave and T is the period of the waveform.
Let us find out the expression for the output.
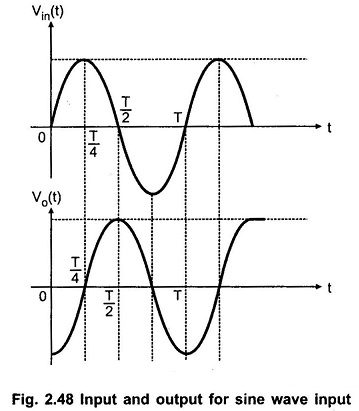
Thus the output of the differentiators is a consine waveform, for a sine wave input. The input and output waveform is shown in the Fig. 2.48.
Disadvantages of an Ideal Op Amp Differentiator:
The gain of the differentiators increases as frequency increases. Thus at some high frequency, the differentiators may become unstable and break into the oscillations. There is possibility that ideal op amp may go into the saturation.
Also the input impedance XC1 = (1/2πfC1) decreases as frequency increases. This makes the circuit very much sensitive to the noise. Thus when such noise gets amplified due to high gain at high frequency, noise may completely override the differentiated output.
Hence the differentiators circuit suffers from the limitations on its stability and noise problems, at high frequencies. These problems can be corrected using some additional parameters in the basic differentiator circuit. Such a differentiators circuit is called practical differentiators circuit.