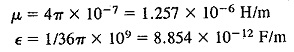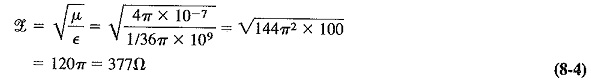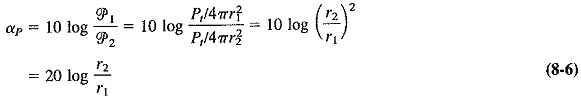Fundamentals of Electromagnetic Waves:
Fundamentals of Electromagnetic Waves are energy propagated through free space at the velocity of light, which is approximately 300 meters per microsecond. As the object travelled downward, there would be a path of bubbles generated in the same direction (vertical) as the object, but there would also be a circular wave pattern radiating from the point of impact and spreading horizontally across the body of water. These two energy reactions approximate (at a very simplistic level) the electromagnetic and electrostatic radiation pattern in free space.
The energy created by the displacement of the liquid is converted into both a vertical and a horizontal component. The energy level of these components varies inversely to the distance; i.e., the horizontal wave-front covers a larger area (considering no losses due to friction obstacles, etc.) and spreads the total energy generated over this expanding wave-front, reducing the energy in any given section dramatically as the wave-front expands and moves away from the point of contact.
This action can be related to the term power density. If power density is defined as radiated power per unit area, it follows that power density is reduced to one-quarter of its value when distance from the source is doubled.
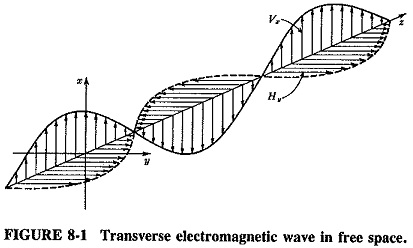
Also, the direction of the electric field, the magnetic field and propagation are mutually perpendicular in Fundamentals of Electromagnetic Waves, as Figure 8-1 shows. This is a theoretical assumption which cannot be “checked,” since the waves are invisible. It may be used to predict the behaviour of Fundamentals of Electromagnetic Waves in all circumstances, such as reflection, refraction and diffraction.
Waves in free space:
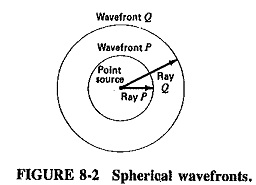
Since no interference or obstacles are present in free space, electromagnetic waves will spread uniformly in all directions from a point source. The wave-front is thus spherical, as shown in cross section in Figure 8-2. To simplify the description even further, “rays” are imagined which radiate from the point source in all directions. They are everywhere perpendicular to a tangential plane of the wave-front, just like the spokes of a wheel.
At the distance corresponding to the length of ray P, the wave has a certain phase. It may have left the source at an instant when its voltage and current were maximum in the circuit feeding the source, i.e., at an instant of maximum electric and magnetic field vectors. If the distance traveled corresponds to exactly 100,000.25 wavelengths, the instantaneous electric and magnetic intensities are at that moment zero of all such points. This is virtually the definition of a wavefront; it is the plane joining all points of identical phase. Here, of course, it is spherical. If the length of ray Q is exactly twice that of ray P, then the area of the new sphere will be exactly four times the area of the sphere with radius P. It is seen that the total power output of the source has spread itself over four times the area when its distance from the source has doubled. If power density is defined as radiated power per unit area, it follows that power density is reduced to one-quarter of its value when distance from the source has doubled.
It is seen that power density is inversely proportional to the square of the distance from the source. This is the inverse-square law, which applies universally to all forms of radiation in free space. Stating this mathematically, we have
where
p = power density at a distance r from an isotrophic source
Pt = transmitted power
An isotropic source is one that radiates uniformly in all directions in space. Although no practical source has this property, the concept of the isotropic radiator is very useful and frequently employed. As a matter of interest, it may be shown quite simply that the inverse-square law applies also when the source is not isotropic, and students are invited to demonstrate this for themselves. However, for wave fronts to\be spherical, the velocity of radiation must be constant at all points (as it is in free space). A propagation medium in which this is true is also called isotropic.
The electric and magnetic field intensities of Fundamentals of Electromagnetic Waves are also important. The two quantities are the direct counterparts of voltage and current in circuits; they are measured in volts per meter and amperes per meter, respectively. Just as for electrical circuits we have V = ZI, so for electromagnetic waves
The characteristic impedance of a medium is given by
where
μ = permeability of medium
ε = electric permittivity of medium
For free space,
It will be recalled that permeability is the equivalent of inductance and permittivity is the equivalent of capacitance in electric circuits; indeed the units used above are a reminder of this. It is now possible to calculate a value for the characteristic impedance of free space. We have, from Equation (8-3)
This makes it possible to calculate the field intensity (field strength) at a distance r from an isotropic source. Just as P = V2/Z in electrical circuits
It is seen from Equation (8-5) that field intensity is inversely proportional to the distance from the source, since it is proportional to the square root of power density.
The wavefront must be considered once again. It is spherical in an isotropic medium, but any small area of it at a large distance from the source may be considered to be a plane wavefront. This can be explained by looking at an everyday example. We know that the earth is spherical as a very close approximation, but we speak of a football field as flat. It represents a finite area of the earth’s surface Fut is at a considerable distance from its center. The concept of plane waves is very useful because it greatly simplifies the treatment of the optical properties of Fundamentals of Electromagnetic Waves, such as reflection and refraction.
Radiation and reception: Antennas radiate electromagnetic waves. Radiation will result from electron flow in a suitable conductor. This is predicted mathematically by the Maxwell equations, which show that current flowing in a wire is accompanied by a magnetic field around it. If the magnetic field is changing, as it does with alternating current, an electric field will be present also.
Polarization: It was illustrated in Figure 8-1 that Fundamentals of Electromagnetic Waves are transverse, and the electric and magnetic fields are at right angles. Since the magnetic field surrounds the wire and is perpendicular to it, it follows that the electric field is parallel to the wire.
Polarization refers to the physical orientation of the radiated waves in space. Waves are said to be polarized (actually linearly polarised) if they all have the same alignment in space. It is a characteristic of most antennas that the radiation they emit is linearly polarized. A vertical antenna will radiate waves whose electric vectors will all be vertical and will remain so in free space. Light emitted by incoherent sources, such as the sun, has a haphazard arrangement of field vectors and is said to be randomly polarized.
The wave of Figure 8-1 is, of course, linearly polarized and is also said to be vertically polarized, since all the electric intensity vectors are vertical. The, decision to label polarization direction after the electric intensity is not as arbitrary as it seems; this makes the direction of polarization the same as the direction of the antenna. Thus, vertical antennas radiate vertically polarized waves, and similarly horizontal antennas produce waves whose polarization is horizontal. There has been a tendency, over the years, to transfer the label to the antenna itself. Thus people often refer to antennas as vertically or horizontally polarized, whereas it is only their radiations that are so polarized.
It is also possible for antenna radiations to be circularly or even elliptically polarized, so that the polarization of the wave rotates continuously in corkscrew fashion.
Reception: Just as a wire carrying HF current is surrounded by electric and magnetic fields, so a wire placed in a moving electromagnetic field will have a current induced in it (basic transformer theory). This is another way of saying that this wire receives some of the radiation and is therefore a receiving antenna. Since the process of reception is exactly the reverse of the process of transmission, transmitting and receiving antennas are basically interchangeable. Apart from power-handling considerations, the two types of antennas are virtually identical. In fact, a so-called principle of reciprocity exists. This principle states that the characteristics of antennas, such as impedance and radiation pattern, are identical regardless of use for reception or transmission, and this relation may be proved mathematically. It is of particular value for antennas employed for both functions.
Attenuation and absorption: The inverse-square law shows that power density diminishes fairly rapidly with distance from the source of Fundamentals of Electromagnetic Waves. Another way of looking at this is to say that electromagnetic waves are attenuated as they travel outward from their source, and this attenuation is proportional to the square of the distance travelled. Attenuation is normally measured in decibels and happens to be the same numerically for both field intensity and power density. This may be shown as follows.
Similarly, for field intensity attenuation, we have
The two formulas are seen to be identical and, in fact, are used in exactly the same way. Thus, at a distance 2r from the source of waves, both field intensity and power density are 6 dB down from their respective values at a distance r from the source.
In free space, of course, absorption of radio waves does not occur because there is nothing there to absorb them. However, the picture is different in the atmosphere. This tends to absorb some radio waves, because some of the energy from the Fundamentals of Electromagnetic Waves is transferred to the atoms and molecules of the atmosphere. This transfer causes the atoms and molecules to vibrate somewhat, and while the atmosphere is warmed only infinitesimally, the energy of the waves may be absorbed quite significantly.
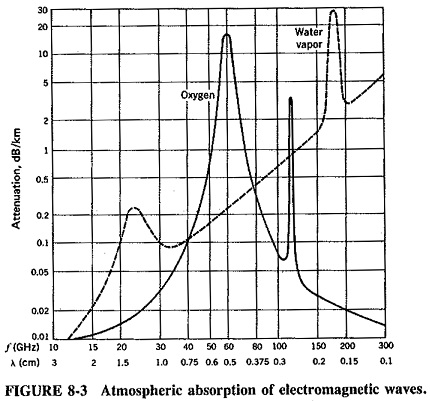
Fortunately, the atmospheric absorption of electromagnetic waves of frequencies below about 10 GHz is quite insignificant. As shown in Figure 8-3, absorption by both the oxygen and the water vapor content of the atmosphere becomes significant at that frequency and then rises gradually. Because of various molecular resonances, however, certain peaks and troughs of attenuation exist. As Figure 8-3 shows, frequencies such as 60 and 120 GHz are not recommended for long-distance propagation in the atmosphere. It is similarly best not to use 23 or 180 GHz either, except in very dry air. So-called windows exist at which absorption is greatly reduced; frequencies such as 33 and 110 GHz fall into this category.
Figure 8-3 shows atmospheric absorption split into its two major components, with absorption due to the water vapor content of the atmosphere taken for a standard value of humidity. If humidity is increased or if there is fog, rain or snow, then this form of absorption is increased tremendously, and reflection from rainwater drops may even take place. For example, a radar system operating at 10 GHz may have a range of 75 km in dry air, 68 ,km in light drizzle, 55 km in light rain, 22 km in moderate rain and 8 km in heavy rain, showing effectively how precipitation causes severe absorption at microwave frequencies. It must be repeated that such absorption is insignificant at lower frequencies, except over very long radio paths.